题目内容
8．在正方体ABCD-A1B1C1D1中，异面直线BC1与CD1所成角的余弦值为（ ）| A． | $-\frac{1}{2}$ | B． | $\frac{{\sqrt{2}}}{2}$ | C． | $\frac{{\sqrt{3}}}{2}$ | D． | $\frac{1}{2}$ |
分析 如图所示，建立空间直角坐标系．利用向量夹角公式即可得出．
解答 解：如图所示，建立空间直角坐标系．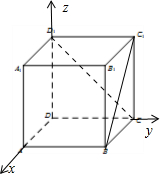
D1（0，0，1），B（1，1，0），C（0，1，0），C1（0，1，1）．
∴$\overrightarrow{C{D}_{1}}$=（0，-1，1），$\overrightarrow{B{C}_{1}}$=（-1，0，1）．
∴$cos＜\overrightarrow{C{D}_{1}}，\overrightarrow{B{C}_{1}}＞$=$\frac{\overrightarrow{C{D}_{1}}•\overrightarrow{B{C}_{1}}}{|\overrightarrow{C{D}_{1}}||\overrightarrow{B{C}_{1}}|}$=$\frac{1}{\sqrt{2}×\sqrt{2}}$=$\frac{1}{2}$．
∴直线A1D与C1E所成角的余弦值是$\frac{1}{2}$．
故选：D．
点评 本题考查了利用向量夹角公式求异面直线所成的夹角方法，考查了推理能力与计算能力，属于基础题．
练习册系列答案
相关题目
18．计算机执行如图的程序段后，输出的结果是（ ）
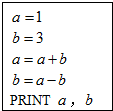
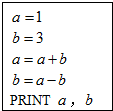
| A． | 1，3 | B． | 4，1 | C． | 4，-2 | D． | 1，-2 |
19．sin$\frac{4π}{3}$=（ ）
| A． | $\frac{{\sqrt{3}}}{2}$ | B． | $\frac{1}{2}$ | C． | $-\frac{{\sqrt{3}}}{2}$ | D． | $-\frac{1}{2}$ |
如图是从上下底面处在水平状态下的棱长为a的正方体ABCD-A1B1C1D1中分离出来的．
13．平行四边形ABCD的对角线AC与BD相交于O，则（ ）
| A． | $\overrightarrow{AB}$+$\overrightarrow{AD}$=$\overrightarrow{DB}$ | B． | $\overrightarrow{OB}$+$\overrightarrow{OC}$=$\overrightarrow{BC}$ | C． | $\overrightarrow{AB}$+$\overrightarrow{BO}$=$\overrightarrow{OC}$ | D． | $\overrightarrow{AB}$-$\overrightarrow{BC}$=$\overrightarrow{BD}$ |
20．向量$\vec a$与向量$\vec a-\vec b$的夹角是$\frac{π}{3}$，$|{\vec a}|=1$，$|{\vec a-\vec b}|=3$，则$|{\vec b}|$等于（ ）
| A． | $\sqrt{6}$ | B． | $\sqrt{7}$ | C． | $2\sqrt{2}$ | D． | 3 |
将数列{an}按如图所示的规律排成一个三角形表，并同时满足以下两个条件：