6.设复数z满足(1-2i)z=3+4i,则z=( )
| A. | 1-2i | B. | -1+2i | C. | 2+i | D. | -2+i |
4.已知双曲线C1:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一个焦点与抛物线C2:x=$\frac{1}{8}$y2的焦点重合,直线l为bx-ay+8=0,P为C2上一个动点,P到直线l的距离为d1,到C2准线的距离为d2,当d1+d2的最小值为5时,C1的方程为( )
| A. | y2-$\frac{{x}^{2}}{3}$=1 | B. | $\frac{{x}^{2}}{3}$-$\frac{{y}^{2}}{4}$=1 | C. | $\frac{{x}^{2}}{3}$-y2=1 | D. | x2-$\frac{{y}^{2}}{3}$=1 |
3.若集合A={x|2${\;}^{{x}^{2}-4x-5}$>1},集合B={x|y=lg$\frac{2-x}{2+x}$},则A∩B=( )
| A. | {x|-5<x<1} | B. | {x|-2<x<1} | C. | {x|-2<x<-1} | D. | {x|-5<x<-1} |
2.已知定义在R上的函数f(x)的导函数为f′(x),满足f′(x)<f(x),f(2)=-2,f(1+x)=-f(1-x),则不等式f(x)<2ex的解集为( )
| A. | (-2,+∞) | B. | (0,+∞) | C. | (1,+∞) | D. | (4,+∞) |
1.函数h(x)=2sin(2x+$\frac{π}{6}$),函数f(x)=2cos(2x-$\frac{2π}{3}$)可由h(x)经过( )的变换得到.
0 246862 246870 246876 246880 246886 246888 246892 246898 246900 246906 246912 246916 246918 246922 246928 246930 246936 246940 246942 246946 246948 246952 246954 246956 246957 246958 246960 246961 246962 246964 246966 246970 246972 246976 246978 246982 246988 246990 246996 247000 247002 247006 247012 247018 247020 247026 247030 247032 247038 247042 247048 247056 266669
| A. | 向右平移$\frac{π}{6}$个单位 | B. | 向左平移$\frac{π}{6}$个单位 | ||
| C. | 向右平移$\frac{π}{3}$个单位 | D. | 向左平移$\frac{π}{3}$个单位 |
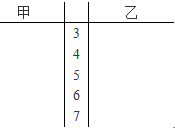 砷是广泛分布于自然界中的非金属元素,长期饮用高砷水会直接危害群众的身心健康和生命安全,而近水农村地区,水质情况更需要关注.为了解甲、乙两地区农村居民饮用水中砷含量的基本情况,分别在两地随机选取10个村子,其砷含量的调查数据如下(单位:mg/1000L):
砷是广泛分布于自然界中的非金属元素,长期饮用高砷水会直接危害群众的身心健康和生命安全,而近水农村地区,水质情况更需要关注.为了解甲、乙两地区农村居民饮用水中砷含量的基本情况,分别在两地随机选取10个村子,其砷含量的调查数据如下(单位:mg/1000L):