题目内容
4.已知双曲线C1:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一个焦点与抛物线C2:x=$\frac{1}{8}$y2的焦点重合,直线l为bx-ay+8=0,P为C2上一个动点,P到直线l的距离为d1,到C2准线的距离为d2,当d1+d2的最小值为5时,C1的方程为( )| A. | y2-$\frac{{x}^{2}}{3}$=1 | B. | $\frac{{x}^{2}}{3}$-$\frac{{y}^{2}}{4}$=1 | C. | $\frac{{x}^{2}}{3}$-y2=1 | D. | x2-$\frac{{y}^{2}}{3}$=1 |
分析 利用双曲线C1:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一个焦点与抛物线C2:x=$\frac{1}{8}$y2的焦点重合,可得a2+b2=4,利用P为C2上一个动点,P到直线l的距离为d1,到C2准线的距离为d2,d1+d2的最小值为5,根据抛物线的定义,可得抛物线的焦点到直线的距离为5,求出a,b,可得双曲线的方程.
解答 解:∵双曲线C1:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一个焦点与抛物线C2:x=$\frac{1}{8}$y2的焦点重合,
∴a2+b2=4,
∵P为C2上一个动点,P到直线l的距离为d1,到C2准线的距离为d2,d1+d2的最小值为5,
∴抛物线的焦点到直线的距离为5,
∴$\frac{|2b+8|}{\sqrt{{b}^{2}+{a}^{2}}}$=5,
∴b=1,∴a=$\sqrt{3}$,
∴C1的方程为$\frac{{x}^{2}}{3}-{y}^{2}=1$.
故选:C.
点评 本题考查抛物线、双曲线的性质,考查抛物线的定义,考查学生的计算能力,正确转化是关键.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
14.双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的离心率为2,焦点到渐近线的距离为$\sqrt{3}$,则C的焦距等于( )
| A. | 2 | B. | 2$\sqrt{2}$ | C. | 2$\sqrt{3}$ | D. | 4 |
19.已知直线m,n和平面α,则m∥n的必要不充分条件是( )
| A. | 直线m,n和平面α成等角 | B. | m⊥α且n⊥α | ||
| C. | m∥α且n?α | D. | m∥α且n∥α |
16.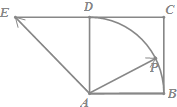 如图,四边形ABCD是正方形,延长CD至E,使DE=CD,若点P是以点A为圆心,AB为半径的圆弧(不超出正方形)上的任一点,设向量$\overrightarrow{AP}=λ\overrightarrow{AB}+μ\overrightarrow{AE}$,则λ+μ的最小值为( )
如图,四边形ABCD是正方形,延长CD至E,使DE=CD,若点P是以点A为圆心,AB为半径的圆弧(不超出正方形)上的任一点,设向量$\overrightarrow{AP}=λ\overrightarrow{AB}+μ\overrightarrow{AE}$,则λ+μ的最小值为( )
 如图,四边形ABCD是正方形,延长CD至E,使DE=CD,若点P是以点A为圆心,AB为半径的圆弧(不超出正方形)上的任一点,设向量$\overrightarrow{AP}=λ\overrightarrow{AB}+μ\overrightarrow{AE}$,则λ+μ的最小值为( )
如图,四边形ABCD是正方形,延长CD至E,使DE=CD,若点P是以点A为圆心,AB为半径的圆弧(不超出正方形)上的任一点,设向量$\overrightarrow{AP}=λ\overrightarrow{AB}+μ\overrightarrow{AE}$,则λ+μ的最小值为( )| A. | $\sqrt{5}$ | B. | 1 | C. | $\sqrt{2}$ | D. | 2 |
13.已知$\frac{\overline z}{i}$=2-i,则在复平面内,复数z对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
 砷是广泛分布于自然界中的非金属元素,长期饮用高砷水会直接危害群众的身心健康和生命安全,而近水农村地区,水质情况更需要关注.为了解甲、乙两地区农村居民饮用水中砷含量的基本情况,分别在两地随机选取10个村子,其砷含量的调查数据如下(单位:mg/1000L):
砷是广泛分布于自然界中的非金属元素,长期饮用高砷水会直接危害群众的身心健康和生命安全,而近水农村地区,水质情况更需要关注.为了解甲、乙两地区农村居民饮用水中砷含量的基本情况,分别在两地随机选取10个村子,其砷含量的调查数据如下(单位:mg/1000L):