9.直线2x-5y+20=0与坐标轴交于两点,以坐标轴为对称轴,以其中一个点为焦点且另一个点为虚轴端点的双曲线的标准方程是( )
| A. | $\frac{{x}^{2}}{84}$-$\frac{{y}^{2}}{16}$=1 | B. | $\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{84}$=1 | ||
| C. | $\frac{{x}^{2}}{100}$-$\frac{{y}^{2}}{84}$=1 | D. | $\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{84}$=1或$\frac{{x}^{2}}{100}$-$\frac{{y}^{2}}{84}$=1 |
7.某同学用“五点法”画函数f(x)=Asin(ωx+φ)+B(A>0,ω>0,|φ|<$\frac{π}{2}$)在某一个周期内的图象时,列表并填入的部分数据如表:
(Ⅰ)请求出表中的x1,x2,x3的值,并写出函数f(x)的解析式;
(Ⅱ)将f(x)的图象向右平移$\frac{2}{3}$个单位得到函数g(x)的图象,若函数g(x)在区间[0,m](3<m<4)上的图象的最高点和最低点分别为M,N,求向量$\overrightarrow{NM}$与$\overrightarrow{ON}$夹角θ的大小.
| x | x1 | $\frac{1}{3}$ | x2 | $\frac{7}{3}$ | x3 |
| ωx+φ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| Asin(ωx+φ)+B | 0 | $\sqrt{3}$ | 0 | -$\sqrt{3}$ | 0 |
(Ⅱ)将f(x)的图象向右平移$\frac{2}{3}$个单位得到函数g(x)的图象,若函数g(x)在区间[0,m](3<m<4)上的图象的最高点和最低点分别为M,N,求向量$\overrightarrow{NM}$与$\overrightarrow{ON}$夹角θ的大小.
1.在平面直角坐标系中,把横、纵坐标均为有理数的点称为有理点.若a为无理数,则在过点P(a,-$\frac{1}{2}$)的所有直线中( )
0 246854 246862 246868 246872 246878 246880 246884 246890 246892 246898 246904 246908 246910 246914 246920 246922 246928 246932 246934 246938 246940 246944 246946 246948 246949 246950 246952 246953 246954 246956 246958 246962 246964 246968 246970 246974 246980 246982 246988 246992 246994 246998 247004 247010 247012 247018 247022 247024 247030 247034 247040 247048 266669
| A. | 有无穷多条直线,每条直线上至少存在两个有理点 | |
| B. | 恰有n(n≥2)条直线,每条直线上至少存在两个有理点 | |
| C. | 有且仅有一条直线至少过两个有理点 | |
| D. | 每条直线至多过一个有理点 |
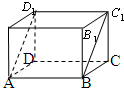 如图,在长方体ABCD-A1B1C1D1中,AB=5,BC=4,AA1=3,沿该长方体对角面ABC1D1将其截成两部分,并将它们再拼成一个新的四棱柱,那么这个四棱柱表面积的最大值为114.
如图,在长方体ABCD-A1B1C1D1中,AB=5,BC=4,AA1=3,沿该长方体对角面ABC1D1将其截成两部分,并将它们再拼成一个新的四棱柱,那么这个四棱柱表面积的最大值为114.