题目内容
1.在平面直角坐标系中,把横、纵坐标均为有理数的点称为有理点.若a为无理数,则在过点P(a,-$\frac{1}{2}$)的所有直线中( )| A. | 有无穷多条直线,每条直线上至少存在两个有理点 | |
| B. | 恰有n(n≥2)条直线,每条直线上至少存在两个有理点 | |
| C. | 有且仅有一条直线至少过两个有理点 | |
| D. | 每条直线至多过一个有理点 |
分析 根据题意,假设一条直线上存在两个有理点,由此推断满足条件的直线有多少即可.
解答 解:设一条直线上存在两个有理点A(x1,y1),B(x2,y2),
由于$P(a,-\frac{1}{2})$也在此直线上,
所以,当x1=x2时,有x1=x2=a为无理数,与假设矛盾,此时该直线不存在有理点;
当x1≠x2时,直线的斜率存在,且有$\frac{{{y_2}-{y_1}}}{{{x_2}-{x_1}}}=\frac{{{y_2}+\frac{1}{2}}}{{{x_2}-a}}$,
又x2-a为无理数,而$\frac{{{y_2}-{y_1}}}{{{x_2}-{x_1}}}$为有理数,
所以只能是${y_2}+\frac{1}{2}=0$,且y2-y1=0,
即${y_2}={y_1}=-\frac{1}{2}$;
所以满足条件的直线只有一条,且直线方程是$y=-\frac{1}{2}$;
所以,正确的选项为C.
故选:C.
点评 本题考查了新定义的关于直线方程与直线斜率的应用问题,解题的关键是理解新定义的内容,寻找解题的途径,是难理解的题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.执行如图所示的程序框图,若a=1,b=2,则输出的结果是( )
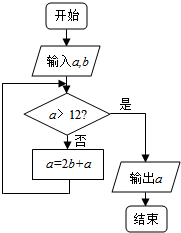

| A. | 9 | B. | 11 | C. | 13 | D. | 15 |
10.四面体ABCD的四个顶点均在半径为2的球面上,若AB、AC、AD两两垂直,$\overrightarrow{BA}•\overrightarrow{BC}$=2,则该四面体体积的最大值为( )
| A. | $\frac{7\sqrt{2}}{6}$ | B. | $\frac{7}{3}$ | C. | 2$\sqrt{2}$ | D. | 7$\sqrt{2}$ |
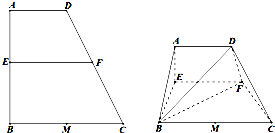 已知梯形ABCD中,AD∥BC,∠ABC=∠BAD=90°,AB=BC=2AD=4,M是BC边的中点,E,F分别是AB,CD上的点,且EF∥BC,设AE=x.如图,沿EF将四边形AEFD折起,使平面AEFD⊥平面EBCF.
已知梯形ABCD中,AD∥BC,∠ABC=∠BAD=90°,AB=BC=2AD=4,M是BC边的中点,E,F分别是AB,CD上的点,且EF∥BC,设AE=x.如图,沿EF将四边形AEFD折起,使平面AEFD⊥平面EBCF.