3．
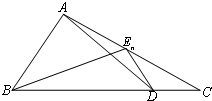如图，已知点D为△ABC的边BC上一点，$\overrightarrow{BD}=3\overrightarrow{DC}$，En（n∈N+）为边AC上的一列点，满足$\overrightarrow{{E_n}A}=\frac{1}{4}{a_{n+1}}\overrightarrow{{E_n}B}-（3{a_n}+2）\overrightarrow{{E_n}D}$，其中实数列{an}中
an＞0，a1=1，则{an}的通项公式为（ ）
如图，已知点D为△ABC的边BC上一点，$\overrightarrow{BD}=3\overrightarrow{DC}$，En（n∈N+）为边AC上的一列点，满足$\overrightarrow{{E_n}A}=\frac{1}{4}{a_{n+1}}\overrightarrow{{E_n}B}-（3{a_n}+2）\overrightarrow{{E_n}D}$，其中实数列{an}中an＞0，a1=1，则{an}的通项公式为（ ）
| A． | 2•3n-1-1 | B． | 2n-1 | C． | 3n-2 | D． | 3•2n-1-2 |
1．下表给出一个等比数阵
其中每行每列都是等比数列，aij
表示第i行第j列的数．
（1）写出a34的值并求出aij的计算公式；
（2）若数列{bn}满足bn=a2n+log2a2n，求数列{bn}的前n项和Sn．
| 1 | 2 | （ ） | （ ） | （ ） | … | a1j | … |
| 3 | 6 | （ ） | （ ） | （ ） | … | a2j | … |
| （ ） | （ ） | （ ） | （ ） | （ ） | … | a3j | … |
| ai1 | ai2 | ai3 | ai4 | ai5 | … | aij | … |
| （ ） | （ ） | （ ） | （ ） | （ ） | … | … | … |
表示第i行第j列的数．
（1）写出a34的值并求出aij的计算公式；
（2）若数列{bn}满足bn=a2n+log2a2n，求数列{bn}的前n项和Sn．
16．函数f（x）=$\left\{\begin{array}{l}{x-sinx，x＞0}\\{{x}^{2}-2014x-2015，x≤0}\end{array}\right.$的零点个数为（ ）
| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
15．若x∈[0，2π]，则sinx+cosx＜1的概率是（ ）
| A． | $\frac{2}{3}$ | B． | $\frac{1}{4}$ | C． | $\frac{3}{4}$ | D． | $\frac{1}{2}$ |
14．已知命题p函数f（x）=$\frac{1}{3}$x3+$\frac{1}{2}$ax2+x有两个极值点；命题q：函数g（x）=x${\;}^{{a}^{2}-a}$在（0，+∞）上为增函数，则p是q的（ ）
0 246833 246841 246847 246851 246857 246859 246863 246869 246871 246877 246883 246887 246889 246893 246899 246901 246907 246911 246913 246917 246919 246923 246925 246927 246928 246929 246931 246932 246933 246935 246937 246941 246943 246947 246949 246953 246959 246961 246967 246971 246973 246977 246983 246989 246991 246997 247001 247003 247009 247013 247019 247027 266669
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |