4.国务院召开青少年校园足球工作电视电话会议,提出教育部将主导校园足球“足球进校园”活动.某市教育部门未了解学生喜欢足球是否与性别有关,在某学校该校50名学生进行了问卷调查,得到了如下的列联表:
(Ⅰ)按性别用分层抽样的方法在喜欢足球的学生中抽取6人,求这6人中男生的人数;
(Ⅱ)在上述抽取的6人中随机抽取2人做进一步调查,求恰有1名女生的概率;
(Ⅲ)根据列联表的独立性检验,能否在犯错误的概率不超过0.01的前提下,认为喜欢足球与性别有关系?
下面的临界值表供参考:
(参考公式:${K}^{2}=\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d)
| 喜欢足球 | 不喜欢足球 | 合计 | |
| 男生 | 20 | 5 | 25 |
| 女生 | 10 | 15 | 25 |
| 合计 | 30 | 20 | 50 |
(Ⅱ)在上述抽取的6人中随机抽取2人做进一步调查,求恰有1名女生的概率;
(Ⅲ)根据列联表的独立性检验,能否在犯错误的概率不超过0.01的前提下,认为喜欢足球与性别有关系?
下面的临界值表供参考:
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| K | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
20.已知角θ的顶点为坐标原点O,始边为x轴的非负半轴,且满足sin$\frac{θ}{2}$=$-\frac{3}{5}$,cos$\frac{θ}{2}$=$\frac{4}{5}$,设B为角θ终边上任意一点,$\overrightarrow{OA}=(0,-1)$,则|$\overrightarrow{OA}-\overrightarrow{OB}$|的取值范围是( )
0 246697 246705 246711 246715 246721 246723 246727 246733 246735 246741 246747 246751 246753 246757 246763 246765 246771 246775 246777 246781 246783 246787 246789 246791 246792 246793 246795 246796 246797 246799 246801 246805 246807 246811 246813 246817 246823 246825 246831 246835 246837 246841 246847 246853 246855 246861 246865 246867 246873 246877 246883 246891 266669
| A. | [$\frac{7}{25},+∞)$ | B. | [$\frac{1}{3}$,+∞) | C. | [$\frac{4}{5}$,+∞) | D. | [1,+∞) |
 已知函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)在一个周期内的图象如图所示,M、N分别是这段图象的最高点和最低点,且$\overrightarrow{OM}•\overrightarrow{ON}$=0(O为坐标原点),则A=$\frac{\sqrt{7}}{12}$π.
已知函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)在一个周期内的图象如图所示,M、N分别是这段图象的最高点和最低点,且$\overrightarrow{OM}•\overrightarrow{ON}$=0(O为坐标原点),则A=$\frac{\sqrt{7}}{12}$π. 某校为宣传环境保护知识,随机抽取了部分学生进行“环境保护知识”测试,所有测试分数的分组区间为[50,70),[70,90),[90,110),[110,130),[130,150].如图是根据抽样测试所得的分数绘制的频率分布直方图.已知样本中分数小于90的人数是36,则样本中分数不小于70且小于130的人数是90.
某校为宣传环境保护知识,随机抽取了部分学生进行“环境保护知识”测试,所有测试分数的分组区间为[50,70),[70,90),[90,110),[110,130),[130,150].如图是根据抽样测试所得的分数绘制的频率分布直方图.已知样本中分数小于90的人数是36,则样本中分数不小于70且小于130的人数是90.

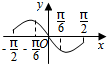

 如图,在矩形ABCD中,AB=2BC,E为线段AB的中点,将△ADE沿直线DE翻折成△A′DE,使平面A′DE⊥平面BCD,F为线段A′C的中点.
如图,在矩形ABCD中,AB=2BC,E为线段AB的中点,将△ADE沿直线DE翻折成△A′DE,使平面A′DE⊥平面BCD,F为线段A′C的中点.