题目内容
19.函数y=x-2sinx在区间[-$\frac{π}{2},\frac{π}{2}$]上的图象大致为( )| A. |  | B. |  | C. | 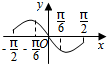 | D. |  |
分析 先判断函数的奇偶性,根据对称性排除A,B,进而把x=$\frac{π}{3}$和$\frac{π}{6}$分别代入,确定大小,排除C.
解答 解:f(-x)═x+2sinx=f(-x),
∴函数为奇函数,故排除A,B,
f($\frac{π}{3}$)=$\frac{π}{3}$-$\sqrt{3}$,f($\frac{π}{6}$)=$\frac{π}{6}$-1
f($\frac{π}{6}$)>f($\frac{π}{3}$),
即在x=$\frac{π}{3}$时,取到最小值,排除C,
故选D.
点评 本题主要考查了正弦函数的图象与性质.考查了学生分析和推理的能力.

练习册系列答案
相关题目
14.已知f(x)定义在R上的函数,f′(x)是f(x)的导函数,若f(x)>1-f′(x),且f(0)=2,则不等式exf(x)>ex+1(其中e为自然对数的底数)的解集为( )
| A. | (0,+∞) | B. | (-∞,0)∪(1,+∞) | C. | (-1,+∞) | D. | (-∞,-1)∪(0,+∞) |
4.国务院召开青少年校园足球工作电视电话会议,提出教育部将主导校园足球“足球进校园”活动.某市教育部门未了解学生喜欢足球是否与性别有关,在某学校该校50名学生进行了问卷调查,得到了如下的列联表:
(Ⅰ)按性别用分层抽样的方法在喜欢足球的学生中抽取6人,求这6人中男生的人数;
(Ⅱ)在上述抽取的6人中随机抽取2人做进一步调查,求恰有1名女生的概率;
(Ⅲ)根据列联表的独立性检验,能否在犯错误的概率不超过0.01的前提下,认为喜欢足球与性别有关系?
下面的临界值表供参考:
(参考公式:${K}^{2}=\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d)
| 喜欢足球 | 不喜欢足球 | 合计 | |
| 男生 | 20 | 5 | 25 |
| 女生 | 10 | 15 | 25 |
| 合计 | 30 | 20 | 50 |
(Ⅱ)在上述抽取的6人中随机抽取2人做进一步调查,求恰有1名女生的概率;
(Ⅲ)根据列联表的独立性检验,能否在犯错误的概率不超过0.01的前提下,认为喜欢足球与性别有关系?
下面的临界值表供参考:
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| K | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
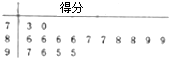 钓鱼岛及其附近海域自古以来就是中国人民进行捕鱼、避风、休息的场所,被誉为深海中的翡翠.某学校就钓鱼岛有关常识随机抽取了16名学生进行测试,用“10分制”以茎叶图方式记录了他们对钓鱼岛的了解程度,分数以小数点前的一位数字为茎,小数点后的一位数字为叶.
钓鱼岛及其附近海域自古以来就是中国人民进行捕鱼、避风、休息的场所,被誉为深海中的翡翠.某学校就钓鱼岛有关常识随机抽取了16名学生进行测试,用“10分制”以茎叶图方式记录了他们对钓鱼岛的了解程度,分数以小数点前的一位数字为茎,小数点后的一位数字为叶.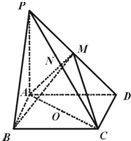 如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=4,AB=2.若M,N分别为棱PD,PC上的点,O为AC的中点,且AC=2OM=2ON.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=4,AB=2.若M,N分别为棱PD,PC上的点,O为AC的中点,且AC=2OM=2ON.