19．对于函数f（x）=x3cos3（x+$\frac{π}{6}$），下列说法正确的是（ ）
| A． | f（x）是奇函数且在（-$\frac{π}{6}$，$\frac{π}{6}$）上递增 | B． | f（x）是奇函数且在（-$\frac{π}{6}$，$\frac{π}{6}$）上递减 | ||
| C． | f（x）是偶函数且在（0，$\frac{π}{6}$）上递增 | D． | f（x）是偶函数且在（0，$\frac{π}{6}$）上递减 |
17．为了解某班学生喜爱打篮球是否与性别有关，对本班50人进行了问卷调查得到了如下的列联表：
己知在全部50人中随机抽取1人抽到不喜爱打篮球的学生的概率为$\frac{2}{5}$．
（1）请将上面的列联表补充完整；
（2）是否有99.5%的把握认为喜爱打篮球与性别有关？说明你的理由：
（3）己知喜爱打篮球的10位女生中，A1，A2，A3还喜欢打乒乓球，B1，B2，B3还喜欢打羽毛球，C1，C2还喜欢踢足球，现在从喜欢打乒乓球、喜欢打羽毛球、喜欢踢足球的8位女生中各选出1名进行其他方面的调查，求B1和C1不全被选中的概率．（下面的临界值表供参考）
（参考公式：K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$，其中n=a+b+c+d）
| 喜爱打篮球 | 不喜爱打篮球 | 合计 | |
| 男生 | 5 | ||
| 女生 | 10 | ||
| 合计 | 50 |
（1）请将上面的列联表补充完整；
（2）是否有99.5%的把握认为喜爱打篮球与性别有关？说明你的理由：
（3）己知喜爱打篮球的10位女生中，A1，A2，A3还喜欢打乒乓球，B1，B2，B3还喜欢打羽毛球，C1，C2还喜欢踢足球，现在从喜欢打乒乓球、喜欢打羽毛球、喜欢踢足球的8位女生中各选出1名进行其他方面的调查，求B1和C1不全被选中的概率．（下面的临界值表供参考）
| p（K2≥k） | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
15．设函数f（x）=sin（ωx+φ）+cos（ωx+φ）（ω＞0，|φ|＜$\frac{π}{2}$）是最小正周期为π的偶函数，则（ ）
0 246493 246501 246507 246511 246517 246519 246523 246529 246531 246537 246543 246547 246549 246553 246559 246561 246567 246571 246573 246577 246579 246583 246585 246587 246588 246589 246591 246592 246593 246595 246597 246601 246603 246607 246609 246613 246619 246621 246627 246631 246633 246637 246643 246649 246651 246657 246661 246663 246669 246673 246679 246687 266669
| A． | f（x）在（0，$\frac{π}{2}$）上单调递减 | B． | f（x）在（$\frac{π}{4}，\frac{3π}{4}$）上单调递减 | ||
| C． | f（x）在（0，$\frac{π}{2}$）上单调递增 | D． | f（x）在（$\frac{π}{4}，\frac{3π}{4}$）上单调递增 |
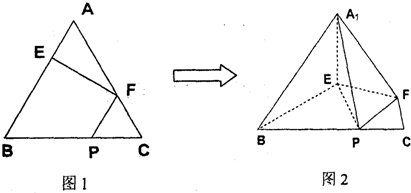
如图，边长为2的正方形ABCD所在平面与圆O所在平面相交于CD，CE为圆O的直径，线段CD为圆O的弦，AE垂直于圆O所在平面，且AE=1