��Ŀ����
17��Ϊ�˽�ij��ѧ��ϲ���������Ƿ����Ա��йأ��Ա���50�˽������ʾ�����õ������µ���������| ϲ�������� | ��ϲ�������� | �ϼ� | |
| ���� | 5 | ||
| �� | 10 | ||
| �ϼ� | 50 |
��1���뽫���������������������
��2���Ƿ���99.5%�İ�����Ϊϲ�����������Ա��йأ�˵��������ɣ�
��3����֪ϲ���������10λŮ���У�A1��A2��A3��ϲ����ƹ����B1��B2��B3��ϲ������ë��C1��C2��ϲ�����������ڴ�ϲ����ƹ����ϲ������ë��ϲ���������8λŮ���и�ѡ��1��������������ĵ��飬��B1��C1��ȫ��ѡ�еĸ��ʣ���������ٽ�ֵ�����ο���
| p��K2��k�� | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
���� ��1���������ݼ��ɽ����������������������
��2�����K2������ٽ�ֵ�������жϼ��ɣ�
��3�������оٷ�������⼴�ɵõ����ۣ�
��� �⣺��1������������£�
| ϲ�������� | ��ϲ�������� | �ϼ� | |
| ���� | 20 | 5 | 25 |
| �� | 10 | 15 | 25 |
| �ϼ� | 30 | 20 | 50 |
��2����${K^2}=\frac{{50��{{��20��15-10��5��}^2}}}{30��20��25��25}��8.333��7.879$������4�֣�
����99.5%�İ�����Ϊϲ�����������Ա��йأ�����6�֣�
��3����ϲ����ƹ����ϲ������ë��ϲ���������8λŮ���и�ѡ1������һ�п��ܵĽ����ɵĻ����¼����£�$\begin{array}{l}��{A_1}��{B_1}��{C_1}������{A_1}��{B_1}��{C_2}������{A_1}��{B_2}��{C_1}������{A_1}��{B_2}��{C_2}������{A_1}��{B_3}��{C_1}������{A_1}��{B_3}��{C_2}����\\��{A_2}��{B_1}��{C_1}������{A_2}��{B_1}��{C_2}������{A_2}��{B_2}��{C_1}������{A_2}��{B_2}��{C_2}������{A_2}��{B_3}��{C_1}������{A_2}��{B_3}��{C_2}����\\��{A_3}��{B_1}��{C_1}������{A_3}��{B_1}��{C_2}������{A_3}��{B_2}��{C_1}������{A_3}��{B_2}��{C_2}������{A_3}��{B_3}��{C_1}������{A_3}��{B_3}��{C_2}����\end{array}$����8�֣�
�����¼�������Ϊ18����M��ʾ��B1��C1��ȫ��ѡ�С���һ�¼���
��������¼�$\overline M$��ʾ��B1��C1ȫ��ѡ�С���һ�¼���
����$\overline M$�ɣ�A1��B1��C1������A2��B1��C1������A3��B1��C1����3�������¼���ɣ�����10�֣�
����$P��\overline M��=\frac{3}{18}=\frac{1}{6}$������11�֣�
�ɶ����¼��ĸ��ʹ�ʽ��$P��\overline M��=1-P��M��=1-\frac{1}{6}=\frac{5}{6}$������12�֣�
���� ������Ҫ��������Լ����Ӧ���Լ��ŵ���͵ĸ��ʵļ��㣬�����оٷ��ǽ������Ĺؼ���

��ϰ��ϵ�д�
�����Ŀ
7����֪ż����f��x����[0��+�ޣ��ϵ�����������f��a+1����f��a-1������ʾ��a��ȡֵ��Χ�ǣ�������
| A�� | ��0��+�ޣ� | B�� | [0��+�ޣ� | C�� | ��-�ޣ�0�� | D�� | ��-1��+�ޣ� |
8����֪����$\overrightarrow{a}$��$\overrightarrow{b}$�ļн�Ϊ$\frac{2��}{3}$��|$\overrightarrow{b}$|=1���Ҷ�����ʵ��x������ʽ|$\overrightarrow{a}$+x$\overrightarrow{b}$|��|$\overrightarrow{a}$+$\overrightarrow{b}$|���������|$\overrightarrow{a}$|=��������
| A�� | $\sqrt{2}$ | B�� | 1 | C�� | 2 | D�� | $\sqrt{3}$ |
9����C���߶�AB�ϣ���|$\overrightarrow{AC}$|=$\frac{5}{2}$|$\overrightarrow{CB}$|����$\overrightarrow{BC}$=k$\overrightarrow{AB}$����k��ֵ�ǣ�������
| A�� | $\frac{5}{7}$ | B�� | -$\frac{5}{7}$ | C�� | -$\frac{2}{7}$ | D�� | $\frac{2}{7}$ |
6����֪����f��x���ĵ�����Ϊf�䣨x��������xf�䣨x��+2f��x��=$\frac{lnx}{x}$����f��e��=$\frac{1}{2e}$����f��x���ڣ�0��+�ޣ��ϵĵ�����Ϊ��������
| A�� | ������� | B�� | �������� | C�� | �����ݼ� | D�� | �ȼ����� |

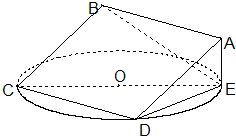 ��ͼ���߳�Ϊ2��������ABCD����ƽ����ԲO����ƽ���ཻ��CD��CEΪԲO��ֱ�����߶�CDΪԲO���ң�AE��ֱ��ԲO����ƽ�棬��AE=1
��ͼ���߳�Ϊ2��������ABCD����ƽ����ԲO����ƽ���ཻ��CD��CEΪԲO��ֱ�����߶�CDΪԲO���ң�AE��ֱ��ԲO����ƽ�棬��AE=1