题目内容
18.在正三角形ABC中,E、F、P分别是-AB、AC、BC边上的点,满足AE:EB=CF:FA=CP:PB=1:2(如图1).将△AEF沿EF折起到△A1EF的位置,使二面角A1-EF-B成直二面角,连结A1B、A1P(如图2)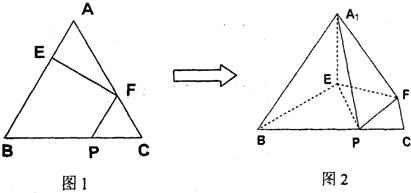
(1)求证:FP∥平面A1EB.
(2)求证:A1E⊥平面BEP;
(3)求直线A1E与平面A1BP所成角的大小.
分析 (1)证明FP∥BE,利用直线与平面平行的判定定理证明FP∥平面A1EB.
(2)不妨设正三角形ABC的边长为3.取BE的中点D,连结DF.证明ADF是正三角形.推出A1EB为二面角A1-EF-B的平面角.证明A1E⊥BE.然后证明A1E⊥平面BEP.
(3)设A1E在平面A1BP内的射影为A1Q,且A1Q交BP于点Q,说明∠EA1Q就是A1E与平面A1BP所成的角,在Rt△A1EQ,求解即可.
解答  (本小题满分14分)
(本小题满分14分)
(1)证明:∵CP:PB=CF:FA,
∴FP∥BE.…(1分)
∵BE?平面A1EB,…(2分)
FP?平面A1EB,…(3分)
∴FP∥平面A1EB.…(4分)
(2)证明:不妨设正三角形ABC 的边长为 3.
在图1中,取BE的中点D,连结DF.
∵AE:EB=CF:FA=1:2,
∴AF=AD=2.…(5分)
而∠A=60°,∴△ADF是正三角形.
又AE=DE=1,∴EF⊥AD.…(6分)
在图2中,A1E⊥EF,BE⊥EF,
∴∠A1EB为二面角A1-EF-B的平面角.…(7分)
由题设条件知此二面角为直二面角,∴A1E⊥BE.
又BE、EF?平面BEF,BE∩EF=E,
∴A1E⊥平面BEF,即A1E⊥平面BEP.…(8分)
(3)在图2中,∵A1E⊥平面BEP,∴A1E⊥BP,
设A1E在平面A1BP内的射影为A1Q,且A1Q交BP于点Q,
则可得BP⊥平面A1EQ,∴BP⊥A1Q.
则∠EA1Q就是A1E与平面A1BP所成的角,…(10分)
在△EBP中,∵BE=BP=2,∠EBP=60°,
∴△EBP是等边三角形,∴BE=EP.
又A1E⊥平面BEP,∴A1B=A1P,∴Q为BP的中点,且EQ=$\sqrt{3}$.…(12分)
又A1E=1,在Rt△A1EQ,tan∠EA1Q=$\frac{EQ}{{{A_1}E}}=\sqrt{3}$,∴∠EA1Q=60°.
所以直线A1E与平面A1BP所成的角为60°.…(14分)
点评 本题考查直线与平面说出来以及二面角的求法,直线与平面垂直的判定定理的应用,考查折叠与展开关系的应用,考查空间想象能力以及计算能力.

 阅读快车系列答案
阅读快车系列答案| A. | {x|1≤x<2} | B. | {x|1<x≤2} | C. | {x|x≥1} | D. | {x|x≤2} |
| A. | $\frac{1}{3}$ | B. | 3 | C. | $\frac{1}{2}$ | D. | 2 |
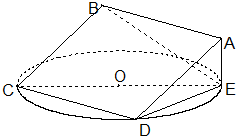 如图,正方形ABCD所在平面与圆O所在平面相交于CD,CE为圆O的直径,线段CD为圆O的弦,AE垂直于圆O所在平面.
如图,正方形ABCD所在平面与圆O所在平面相交于CD,CE为圆O的直径,线段CD为圆O的弦,AE垂直于圆O所在平面.