4.已知某空间几何体的三视图如右图所示,则该几何体的体积是( )

| A. | 16 | B. | 32 | C. | 32 | D. | 48 |
3.已知在圆x2+y2-4x+2y=0内,过点E(1,0)的最长弦和最短弦分别是AC和BD,则四边形ABCD的面积为( )
| A. | $3\sqrt{5}$ | B. | 6$\sqrt{5}$ | C. | $4\sqrt{15}$ | D. | 2$\sqrt{15}$ |
2.执行如图所示程序框图,则输出a=( )


| A. | 20 | B. | 14 | C. | 10 | D. | 7 |
1.已知函数f(x)=log2x,若在[1,8]上任取一个实数x0,则不等式1≤f(x0)≤2成立的概率是( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{7}$ | D. | $\frac{1}{2}$ |
19.某校高一年级有四个班,其中一、二班为数学课改班,三、四班为数学非课改班.在期末考试中,课改班与非课改班的数学成绩优秀与非优秀人数统计如表.
(1)请完成上面的2×2列联表,并判断若按99%的可靠性要求,能否认为“成绩与课改有关”;
(2)若采用分层抽样的方法从课改班的学生中随机抽取4人,则数学成绩优秀和数学成绩非优秀抽取的人数分别是多少?
(3)在(2)的条件下,从中随机抽取2人,求两人数学成绩都优秀的概率.
| 优秀 | 非优秀 | 总计 | |
| 课改班 | 50 | ||
| 非课改班 | 20 | 110 | |
| 合计 | 210 |
(2)若采用分层抽样的方法从课改班的学生中随机抽取4人,则数学成绩优秀和数学成绩非优秀抽取的人数分别是多少?
(3)在(2)的条件下,从中随机抽取2人,求两人数学成绩都优秀的概率.
18.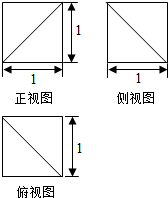 某几何体的三视图如图所示,则该几何体的体积是( )
某几何体的三视图如图所示,则该几何体的体积是( )
 某几何体的三视图如图所示,则该几何体的体积是( )
某几何体的三视图如图所示,则该几何体的体积是( )| A. | $\frac{5}{6}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{6}$ |
17.某校高一年级有四个班,其中一、二班为数学课改班,三、四班为数学非课改班.在期末考试中,课改班与非课改班的数学成绩优秀与非优秀人数统计如表.
(1)请完成上面的2×2列联表,并判断若按99%的可靠性要求,能否认为“成绩与课改有关”;
(2)把全部210人进行编号,从编号中有放回抽取4次,每次抽取1个,记被抽取的4人中的优秀人数为ξ,若每次抽取的结果是相互独立的,求ξ的分布列及数学期望Eξ.
0 245808 245816 245822 245826 245832 245834 245838 245844 245846 245852 245858 245862 245864 245868 245874 245876 245882 245886 245888 245892 245894 245898 245900 245902 245903 245904 245906 245907 245908 245910 245912 245916 245918 245922 245924 245928 245934 245936 245942 245946 245948 245952 245958 245964 245966 245972 245976 245978 245984 245988 245994 246002 266669
| 优秀 | 非优秀 | 总计 | |
| 课改班 | 50 | ||
| 非课改班 | 20 | 110 | |
| 合计 | 210 |
(2)把全部210人进行编号,从编号中有放回抽取4次,每次抽取1个,记被抽取的4人中的优秀人数为ξ,若每次抽取的结果是相互独立的,求ξ的分布列及数学期望Eξ.