题目内容
18．
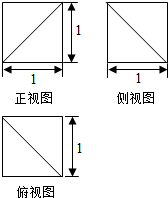某几何体的三视图如图所示，则该几何体的体积是（ ）| A． | $\frac{5}{6}$ | B． | $\frac{2}{3}$ | C． | $\frac{1}{2}$ | D． | $\frac{1}{6}$ |
分析 根据几何体的三视图，得出该几何体是一正方体去掉一个三棱锥，结合图中数据求出它的体积．
解答 解：根据几何体的三视图，得；
该几何体是一棱长为1的正方体，去掉一三棱锥，
如图所示；
∴该几何体的体积是V几何体=13-$\frac{1}{3}×$$\frac{1}{2}$×12×1=$\frac{5}{6}$．
故选：A．
点评 本题考查了利用空间几何体的三视图求体积的应用问题，是基础题目．
练习册系列答案
相关题目
8．某单位为了了解用电量y（度）与当天平均气温x（℃）之间的关系，随机统计了某4天的当天平均气温与用电量（如表）．由数据运用最小二乘法得线性回归方程$\widehaty=-2•x+a$，则a=60．
| 平均气温x（℃） | 18 | 13 | 10 | -1 |
| 用电量y（度） | 25 | 35 | 37 | 63 |
9．函数f（x）=|sin$\frac{x}{2}$cos$\frac{x}{2}$|的最小正周期是（ ）
| A． | $\frac{π}{4}$ | B． | $\frac{π}{2}$ | C． | π | D． | 2π |
3．已知在圆x2+y2-4x+2y=0内，过点E（1，0）的最长弦和最短弦分别是AC和BD，则四边形ABCD的面积为（ ）
| A． | $3\sqrt{5}$ | B． | 6$\sqrt{5}$ | C． | $4\sqrt{15}$ | D． | 2$\sqrt{15}$ |
10．函数f（x）=sin（ωx+φ）（ω＞0，|φ|≤$\frac{π}{3}$）的最小正周期是π，若其图象向右平移$\frac{π}{3}$个单位后得到的函数为奇函数，则函数f（x）（ ）
| A． | 关于点（$\frac{π}{12}$，0）对称 | B． | 关于点（$\frac{5π}{12}$，0）对称 | ||
| C． | 关于直线x=$\frac{5π}{12}$对称 | D． | 关于直线x=$\frac{π}{12}$对称 |
7．已知tanθ=-3，θ∈（$\frac{3}{2}$π，2π），则3sinθ-cosθ的值为（ ）
| A． | $\frac{4}{5}$$\sqrt{10}$ | B． | -$\frac{4}{5}$$\sqrt{10}$ | C． | -$\sqrt{10}$ | D． | $\frac{2}{5}$$\sqrt{10}$ |
如图，已知△ABC是等腰直角三角形，CA=1，点P是△ABC内一点，过点P分别引三边的平行线，与各边围成以P为顶点的三个三角形（图中阴影部分）．