题目内容
3.已知在圆x2+y2-4x+2y=0内,过点E(1,0)的最长弦和最短弦分别是AC和BD,则四边形ABCD的面积为( )| A. | $3\sqrt{5}$ | B. | 6$\sqrt{5}$ | C. | $4\sqrt{15}$ | D. | 2$\sqrt{15}$ |
分析 圆x2+y2-4x+2y=0即(x-2)2+(y+1)2=5,圆心M(2,-1),半径r=$\sqrt{5}$,最长弦AC为圆的直径.BD为最短弦,AC与BD相垂直,求出BD,由此能求出四边形ABCD的面积.
解答 解:圆x2+y2-4x+2y=0即(x-2)2+(y+1)2=5,圆心M(2,-1),半径r=$\sqrt{5}$,
最长弦AC为圆的直径为2$\sqrt{5}$,
∵BD为最短弦
∴AC与BD相垂直,ME=d=$\sqrt{2}$,
∴BD=2BE=2$\sqrt{5-2}$=2$\sqrt{3}$,
∵S四边形ABCD=S△ABD+S△BDC=$\frac{1}{2}$BD×EA+$\frac{1}{2}$×BD×EC
=$\frac{1}{2}$×BD×(EA+EC)=$\frac{1}{2}$×BD×AC=$\frac{1}{2}×2\sqrt{3}×2\sqrt{5}$=2$\sqrt{15}$.
故选:D
点评 本题考查四边形的面积的求法,是中档题,解题时要认真审题,注意圆的性质的合理运用.

练习册系列答案
相关题目
18.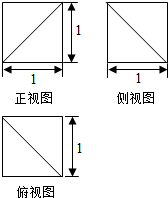 某几何体的三视图如图所示,则该几何体的体积是( )
某几何体的三视图如图所示,则该几何体的体积是( )
 某几何体的三视图如图所示,则该几何体的体积是( )
某几何体的三视图如图所示,则该几何体的体积是( )| A. | $\frac{5}{6}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{6}$ |
8.复数$\frac{1}{1-i}$(i是虚数单位)的虚部是( )
| A. | 1 | B. | i | C. | $\frac{1}{2}$ | D. | $\frac{1}{2}$i |