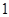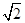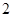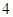题目内容
已知 ,
, ,
, ,且
,且 ,其中
,其中
(1)若 与
与 的夹角为
的夹角为 ,求
,求 的值;
的值;
(2)记 ,是否存在实数
,是否存在实数 ,使得
,使得 对任意的
对任意的 恒成立?若存在,求出实数
恒成立?若存在,求出实数 的取值范围;若不存在,试说明理由.
的取值范围;若不存在,试说明理由.
 ,
, ,
, ,且
,且 ,其中
,其中
(1)若
 与
与 的夹角为
的夹角为 ,求
,求 的值;
的值;(2)记
 ,是否存在实数
,是否存在实数 ,使得
,使得 对任意的
对任意的 恒成立?若存在,求出实数
恒成立?若存在,求出实数 的取值范围;若不存在,试说明理由.
的取值范围;若不存在,试说明理由.(1)1;(2)不存在
试题分析:(1)先运用向量的数量积公式求出
 ,对式子
,对式子 两边平方以及结合
两边平方以及结合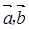 的模均是1得到关于
的模均是1得到关于 的等式
的等式 ;(2)利用(1)中
;(2)利用(1)中 平方求出的式子将
平方求出的式子将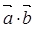 表示成关于
表示成关于 的式子
的式子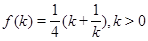 ,均值不等式求得
,均值不等式求得 ,再利用
,再利用 解得
解得 .
.(1)
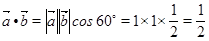 ,由
,由 ,
,
得
 ,即
,即
 (6分)
(6分)由(1)得,
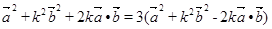
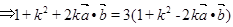 ,即可得,
,即可得,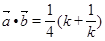
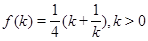 ,因为
,因为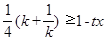 对于任意
对于任意 恒成立,又因为
恒成立,又因为 ,所以
,所以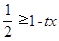 ,即
,即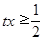 对于任意
对于任意 恒成立,构造函数
恒成立,构造函数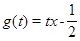
从而
 由此可知不存在实数
由此可知不存在实数 使之成立.
使之成立.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
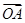 =2a-b,
=2a-b,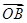 =3a+b,
=3a+b,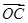 =a-3b,求证:A、B、C三点共线;
=a-3b,求证:A、B、C三点共线;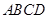 中,下列结论中正确的是( )
中,下列结论中正确的是( ) 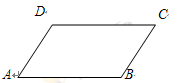
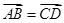
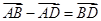
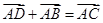
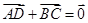
 为
为 所在平面上的一点,且
所在平面上的一点,且 ,其中
,其中 为实数,若点
为实数,若点



 中,
中,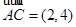 ,
,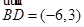 ,则该四边形的面积为( ).
,则该四边形的面积为( ). 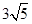
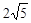
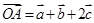 ,
,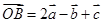 ,
,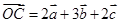 ,
,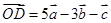 ,其中
,其中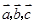 三向量不共面.试判断A,B,C,D四点是否共面?
三向量不共面.试判断A,B,C,D四点是否共面?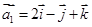 ,
,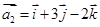 ,
,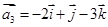 ,
,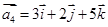 .试问是否存在实数
.试问是否存在实数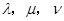 ,使
,使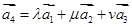 成立?如果存在,求出
成立?如果存在,求出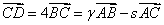 ,则s+r等于( )
,则s+r等于( )
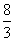
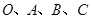 ,若
,若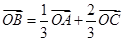 ,则
,则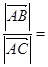 .
.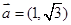 ,
,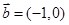 ,则
,则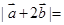 ( )
( )