题目内容
设a、b是不共线的两个非零向量，
(1)若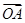
＝2a－b，
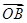＝3a＋b，
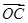＝a－3b，求证：A、B、C三点共线；
(2)若8a＋kb与ka＋2b共线，求实数k的值．
(1)若
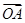＝2a－b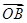，＝3a＋b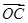，＝a－3b，求证：A、B、C三点共线；(2)若8a＋kb与ka＋2b共线，求实数k的值．
（1）见解析 （2）±4
解：(1)∵
＝(3a＋b)－(2a－b)＝a＋2b，
而
＝(a－3b)－(3a＋b)＝－2a－4b＝－2，
∴与共线，且有公共端点B.
∴A、B、C三点共线．
(2)∵8a＋kb与ka＋2b共线，
∴存在实数λ，使得
(8a＋kb)＝λ(ka＋2b)
⇒(8－λk)a＋(k－2λ)b＝0.
∵a与b不共线，
∴
⇒8＝2λ2⇒λ＝±2.
∴k＝2λ＝±4.
＝(3a＋b)－(2a－b)＝a＋2b，而
＝(a－3b)－(3a＋b)＝－2a－4b＝－2，∴
与共线，且有公共端点B.∴A、B、C三点共线．
(2)∵8a＋kb与ka＋2b共线，
∴存在实数λ，使得
(8a＋kb)＝λ(ka＋2b)
⇒(8－λk)a＋(k－2λ)b＝0.
∵a与b不共线，
∴
⇒8＝2λ2⇒λ＝±2.∴k＝2λ＝±4.
练习册系列答案
导学教程高中新课标系列答案
相关题目
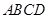中，已知
，
，则
的值是 .
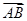＝(6,1)，
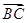＝(x，y)，
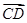＝(－2，－3)，若
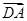且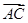
⊥
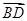，则四边形ABCD的面积S为( )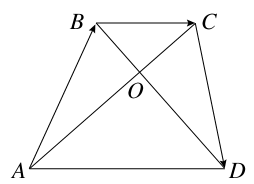
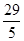
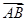与向量a＝(2,3)同向，且|
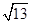，则点B的坐标为( )
＋
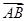＝0，(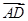
)·
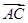＝0，则该四边形一定是( )
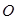为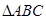
所在平面内一点，满足
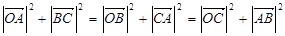，则点
，
，
，且
，其中
，求
的值；
，是否存在实数
，使得
对任意的
恒成立？若存在，求出实数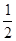
，ｍ）三点共线，则ｍ的值（ ）.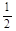 
，
，
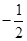
，则
_________________.