题目内容
7.由抛物线y2=$\frac{x}{5}$,y2=x-1所围成封闭图形的面积为$\frac{2}{3}$.分析 联立方程,先求出其交点坐标,再利用微积分基本定理定理即可得出
解答 解:如图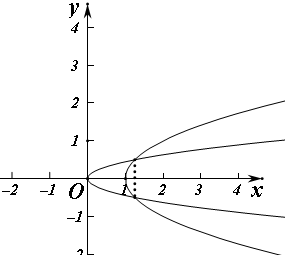 两个曲线的交点为(1.25,±0.5),
两个曲线的交点为(1.25,±0.5),
所以由抛物线y2=$\frac{x}{5}$,y2=x-1所围成封闭图形的面积为:2${∫}_{0}^{\frac{1}{2}}({y}^{2}+1-5{y}^{2})dy$=2${∫}_{0}^{\frac{1}{2}}(1-4{y}^{2})dy$=2(y-$\frac{4}{3}{y}^{3}$)|${\;}_{0}^{\frac{1}{2}}$=$\frac{2}{3}$;
故答案为:$\frac{2}{3}$.
点评 本题考查了定积分的应用,正确求导积分变量以及变量范围,熟练掌握微积分基本定理定理是解题的关键.

练习册系列答案
相关题目
17.设复数z=$\frac{3i-a}{i}$,若复数z在复平面内对应的点在第一象限是a>-1的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
2.已知y=log3(3x+1)+ax是偶函数,y=b+$\frac{2}{{e}^{x}-1}$为奇函数,则a+b=( )
| A. | -1 | B. | 0 | C. | $\frac{1}{2}$ | D. | 1 |
19.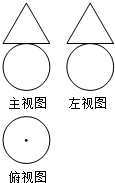 某几何体的三视图如图所示,其中三角形的三边长与圆的直径均为2,则该几何体的表面积为( )
某几何体的三视图如图所示,其中三角形的三边长与圆的直径均为2,则该几何体的表面积为( )
 某几何体的三视图如图所示,其中三角形的三边长与圆的直径均为2,则该几何体的表面积为( )
某几何体的三视图如图所示,其中三角形的三边长与圆的直径均为2,则该几何体的表面积为( )| A. | $\frac{4+\sqrt{3}}{3}$π | B. | 5π | C. | 6π | D. | 7π |
16.若f(x)=sin(2x+φ)为偶函数,则φ值可能是( )
| A. | $\frac{π}{4}$ | B. | $\frac{π}{2}$ | C. | $\frac{π}{3}$ | D. | π |