题目内容
12.计算:S=$\sqrt{1+\frac{1}{{1}^{2}}+\frac{1}{{2}^{2}}}$+$\sqrt{1+\frac{1}{{2}^{2}}+\frac{1}{{3}^{2}}}$+…+$\sqrt{1+\frac{1}{10{0}^{2}}+\frac{1}{10{1}^{2}}}$的值为$\frac{10200}{101}$.分析 由题意设${a}_{n}=1+\frac{1}{{n}^{2}}+\frac{1}{(n+1)^{2}}$,同分后化简凑成完全平方式并求出$\sqrt{{a}_{n}}$,再利用裂项相消法求出式子S的值.
解答 解:由题意设${a}_{n}=1+\frac{1}{{n}^{2}}+\frac{1}{(n+1)^{2}}$=1+$\frac{{(n+1)}^{2}+{n}^{2}}{{n}^{2}(n+1)^{2}}$
=1+$\frac{2{n}^{2}+2n+1}{{n}^{2}(n+1)^{2}}$=1+$\frac{2n(n+1)+1}{{n}^{2}{(n+1)}^{2}}$=1+$\frac{2}{n(n+1)}+$$\frac{1}{{n}^{2}{(n+1)}^{2}}$
=$[1+\frac{1}{n(n+1)}]^{2}$,
∴$\sqrt{{a}_{n}}$=1+$\frac{1}{n(n+1)}$=1+$\frac{1}{n}-\frac{1}{n+1}$,
∴S=$\sqrt{1+\frac{1}{{1}^{2}}+\frac{1}{{2}^{2}}}$+$\sqrt{1+\frac{1}{{2}^{2}}+\frac{1}{{3}^{2}}}$+…+$\sqrt{1+\frac{1}{10{0}^{2}}+\frac{1}{10{1}^{2}}}$
=100+(1$-\frac{1}{2}$)+($\frac{1}{2}-\frac{1}{3}$)+…+($\frac{1}{100}-$$\frac{1}{101}$)
=100+1-$\frac{1}{101}$=$\frac{10{1}^{2}-1}{101}=\frac{10200}{101}$,
故答案为:$\frac{10200}{101}$.
点评 本题考查构造数列法,以及裂项相消法求数列的前n项和,考查化简、变形能力,属于中档题.

 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案| A. | y=-2 | B. | 9x+y-16=0 | C. | 9x+y-16=0或y=-2 | D. | 9x-y-16=0 |
| A. | R | B. | (-∞,-2)∪($\frac{2}{3}$,+∞) | C. | (-$\frac{2}{3}$,2) | D. | (-2,$\frac{2}{3}$) |
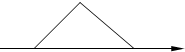 用斜二测画法得到某三角形的水平放置的直观图是一个等腰直角三角形(如图所示,其中的x轴表示水平方向),斜边长为2,则原三角形的面积为( )
用斜二测画法得到某三角形的水平放置的直观图是一个等腰直角三角形(如图所示,其中的x轴表示水平方向),斜边长为2,则原三角形的面积为( )| A. | $\sqrt{2}$ | B. | 2$\sqrt{2}$ | C. | 2 | D. | 4 |
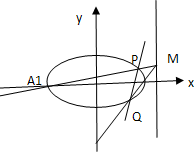 已知椭圆C的中心在坐标原点,焦点在x轴上,椭圆上的点到焦点的距离的最小值为2-$\sqrt{3}$,其离心率e是方程2x2-3$\sqrt{3}$x+3=0的根.
已知椭圆C的中心在坐标原点,焦点在x轴上,椭圆上的点到焦点的距离的最小值为2-$\sqrt{3}$,其离心率e是方程2x2-3$\sqrt{3}$x+3=0的根.