题目内容
16.已知函数f(x)=ax2-(b-1)x+1,其中a∈(-2,0),b∈R.(1)当a=-1时,解不等式f(x)+f(-x)+3x>0;
(2)若函数f(x)在区间(-2,-1)内恰有一个零点,求a-b的取值范围;
(3)设b>1,当函数f(x)的定义域为[1a,−1a]时,值域为[32a,-3a],求a,b.
分析 (1)当a=-1时,不等式可化为-2x2+3x+2>0,从而解得;
(2)由a∈(-2,0),b∈R知△=(b-1)2-4a>0,从而可得f(-2)f(-1)<0,即(4a+2b-1)(a+b)<0,再设m=a-b,b=a-m,从而由线性规划可得0<-m<132,从而解得;
(3)函数f(x)=ax2-(b-1)x+1的对称轴x=b−12a<0,且开口向下,从而讨论以确定函数的最值,从而代入求解即可.
解答 解:∵f(x)=ax2-(b-1)x+1,
∴f(-x)=ax2+(b-1)x+1,
(1)当a=-1时,
∵f(x)+f(-x)+3x>0;
∴-2x2+3x+2>0,
即2x2-3x-2<0,
解得,−12<x<2;
(2)∵a∈(-2,0),b∈R.
∴△=(b-1)2-4a>0,
∴函数f(x)=ax2-(b-1)x+1的图象与x轴有2个交点,
∵函数f(x)在区间(-2,-1)内恰有一个零点,
∴f(-2)f(-1)<0,
即(4a+2b-1)(a+b)<0,
设m=a-b,b=a-m,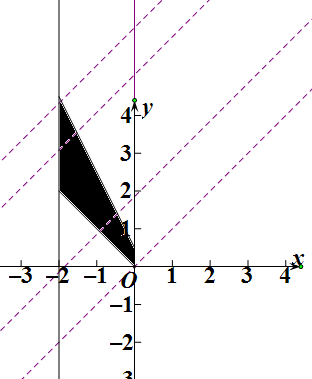
由图象可得:过(0,0)的直线的截距为0,
过(-2,92)的直线的截距为132,
∴0<-m<132,
即-132<m<0,
故a-b的范围为(-132,0);
(3)∵函数f(x)=ax2-(b-1)x+1,
∴对称轴x=b−12a<0,
当1<b<3时,22a<b−12a,
∴f(b−12a)=-3a,f(-1a)=32a,
即(b-1)2-4a+12a2=0,a+b=32;
解得,a=-12,b=2;
当b≥3时,b−12a<22a,
∴f(1a)=-3a,f(-1a)=32a,
即2-b+a+3a2=0,a+b=32;
无解;
综上所述,a=-12,b=2.
点评 本题考查了函数的综合应用及线性规划的应用,同时考查了二次函数的性质与应用,属于中档题.

| A. | 假设a,b,c中只有一个为0 | B. | 假设a,b,c都不为0 | ||
| C. | 假设a,b,c都为0 | D. | 假设a,b,c不都为0 |
| A. | [-1,15] | B. | [-1,9] | C. | [3,15] | D. | [0,9] |

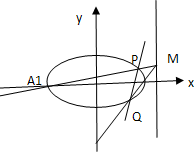 已知椭圆C的中心在坐标原点,焦点在x轴上,椭圆上的点到焦点的距离的最小值为2-
已知椭圆C的中心在坐标原点,焦点在x轴上,椭圆上的点到焦点的距离的最小值为2-