题目内容
【题目】如图,ABC为一直角三角形草坪,其中∠C=90°,BC=2米,AB=4米,为了重建草坪,设计师准备了两套方案: 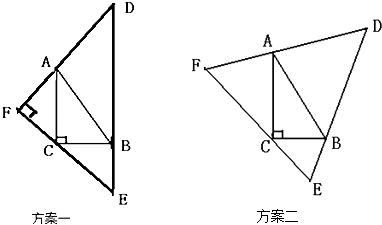
方案一:扩大为一个直角三角形,其中斜边DE过点B,且与AC平行,DF过点A,EF过点C;
方案二:扩大为一个等边三角形,其中DE过点B,DF过点A,EF过点C.
(1)求方案一中三角形DEF面积S1的最小值;
(2)求方案二中三角形DEF面积S2的最大值.
【答案】
(1)解:在方案一:在三角形AFC中,设∠ACF=α,α∈(0, ![]() ),
),
则 ![]() ,
,
因为DE∥AC,所以∠E=α, ![]() ,
,
且 ![]() ,即
,即 ![]() ,
,
解得 ![]() ,
,
所以 ![]() ,
,
所以当sin2α=1,即α=45°时,S1有最小值 ![]()
(2)解:在方案二:在三角形DBA中,设∠DBA=β,β∈(0, ![]() ),则
),则 ![]() ,
,
解得 ![]() ,
,
三角形CBE中,有 ![]() ,解得
,解得 ![]() ,
,
则等边三角形的边长为 ![]()
所以边长的最大值为 ![]() ,所以面积S2的最大值为
,所以面积S2的最大值为 ![]()
【解析】(1)在方案一:在三角形AFC中,设∠ACF=α,α∈(0, ![]() ),表示出三角形DEF面积S1 , 利用基本不等式求出最小值;(2)在方案二:在三角形DBA中,设∠DBA=β,β∈(0,
),表示出三角形DEF面积S1 , 利用基本不等式求出最小值;(2)在方案二:在三角形DBA中,设∠DBA=β,β∈(0, ![]() ),表示出三角形DEF面积S1 , 利用辅助角公式求出最小值.
),表示出三角形DEF面积S1 , 利用辅助角公式求出最小值.
【考点精析】关于本题考查的基本不等式在最值问题中的应用,需要了解用基本不等式求最值时(积定和最小,和定积最大),要注意满足三个条件“一正、二定、三相等”才能得出正确答案.

练习册系列答案
相关题目