Question

【题目】已知函数，关于的不等式只有两个整数解，则实数的取值范围是（ ）

A. B. C. D.

Answer 1

【答案】A

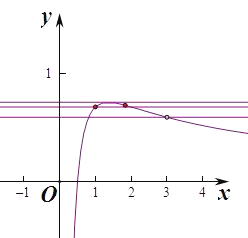
【解析】函数f(x)的定义域为(0,+∞)，则，

当f′(x)>0得1ln(2x)>0,即ln(2x)<1，即0<2x<e,即，

由f′(x)<0得1ln(2x)<0,得ln(2x)>1，即2x>e,即，

即当时,函数f(x)取得极大值,同时也是最大值，

即当时, 有一个整数解1，

当时, 有无数个整数解，

若a=0,则f2(x)+af(x)>0得f2(x)>0，此时有无数个整数解，不满足条件。

若a>0，则由f2(x)+af(x)>0得f(x)>0或f(x)<a，

当f(x)>0时，不等式有无数个整数解，不满足条件。

当a<0时,由f2(x)+af(x)>0得f(x)>a或f(x)<0，

当f(x)<0时，没有整数解，

则要使当f(x)>a有两个整数解，

∵，

∴当f(x)ln2时,函数有两个整数点1,2,当时，函数有3个整数点1，2，3，

∴要使f(x)>a有两个整数解，则，即，

本题选择A选项.