题目内容
13.当函数y=2cosx-3sinx取得最大值时,tanx的值是-$\frac{3}{2}$.分析 用辅助角法将原函数转化为y=$\sqrt{13}$sin(φ-x)(其中tanφ=$\frac{2}{3}$).再应用整体思想求解.
解答 解:y=2cosx-3sinx=$\sqrt{13}$sin(φ-x)(其中tanφ=$\frac{2}{3}$).
y有最大值时,应sin(φ-x)=1⇒φ-x=2kπ+$\frac{π}{2}$⇒-x=2kπ+$\frac{π}{2}$-φ.
∴tanx=-tan(-x)=-tan(2kπ+$\frac{π}{2}$-φ)=-cotφ=-$\frac{1}{tanφ}$=-$\frac{3}{2}$.
故答案为:-$\frac{3}{2}$.
点评 本题主要考查在三角函数中用辅助角法将一般的函数转化为一个角的一种三角函数,用整体思想来应用三角函数的性质解题.

练习册系列答案
相关题目
18.设f(x)是定义在R上的偶函数,且当x≥0时,f(x)=$\left\{\begin{array}{l}{{x}^{2}-1,0≤x<1}\\{lnx,x≥1}\end{array}\right.$,若对任意的x∈[a,a+1],不等式f(2x)≤f(x+a)恒成立,则实数a的最大值为( )
| A. | -1 | B. | -$\frac{2}{3}$ | C. | -$\frac{1}{2}$ | D. | -$\frac{3}{4}$ |
 ,
,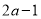 ,
,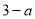 .则这个数列的通项公式为_______.
.则这个数列的通项公式为_______. :
: (
(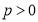 )与椭圆
)与椭圆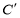 :
: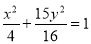 相交所得的弦长为
相交所得的弦长为
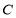 的标准方程;
的标准方程;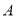 ,
,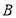 是
是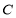 上异于原点
上异于原点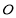 的两个不同点,直线
的两个不同点,直线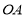 和
和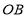 的倾斜角分别为
的倾斜角分别为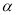 和
和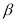 ,当
,当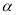 ,
,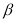 变化且
变化且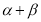 为定值
为定值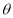 (
(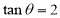 )时,证明:直线
)时,证明:直线 恒过定点,并求出该定点的坐标.
恒过定点,并求出该定点的坐标.