题目内容
8.数列{$\sqrt{n}$-$\sqrt{n+1}$}的前99项和为-9.分析 写出每一项,并项相加即可.
解答 解:($\sqrt{1}$-$\sqrt{2}$)+($\sqrt{2}$-$\sqrt{3}$)+($\sqrt{3}$-$\sqrt{4}$)+…+($\sqrt{98}$-$\sqrt{99}$)+($\sqrt{99}$-$\sqrt{100}$)
=$\sqrt{1}$-$\sqrt{100}$
=-9,
故答案为:-9.
点评 本题考查数列的求和,利用并项法是解决本题的关键,属于基础题.

练习册系列答案
相关题目
5.已知复数z=x+yi(x,y∈R),且有$\frac{x}{i-1}$=1+yi,$\overline z$是z的共轭复数,那么$\frac{1}{\overline{z}}$的虚部为( )
| A. | -$\frac{1}{5}$i | B. | $\frac{1}{5}$ | C. | -$\frac{1}{5}$ | D. | $\frac{1}{5}$i |
 ,
,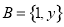 ,且
,且 ,则
,则 ( )
( )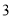 B.
B.
 D.
D.