题目内容
3.数列{an}的前n项和为Sn,已知a1=$\frac{1}{2}$,Sn=n2an-n(n-1),n=1,2,…,求Sn关于n的表达式.分析 当n≥2时,Sn=n2an-n(n-1),把an=Sn-Sn-1代入化为$\frac{n+1}{n}$Sn-$\frac{n}{n-1}$Sn-1=1,利用等差数列的通项公式即可得出.
解答 解:当n≥2时,Sn=n2an-n(n-1),
∴Sn=n2(Sn-Sn-1)-n(n-1),
化为$\frac{n+1}{n}$Sn-$\frac{n}{n-1}$Sn-1=1,
∴数列{$\frac{n+1}{n}$Sn}是等差数列,首项为1,公差为1,
∴$\frac{n+1}{n}$Sn=1+n-1=n,
∴Sn=$\frac{{n}^{2}}{n+1}$.
点评 本题考查了递推式的应用、等差数列的通项公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
14.已知圆x2+y2=4,点A($\sqrt{3}$,0),动点M在圆上运动,O为坐标原点,则∠OMA的最大值为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
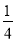 圆弧)( )
圆弧)( )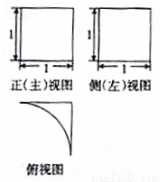
 B.
B.
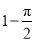 D.
D.