题目内容
18.设f(x)是定义在R上的偶函数,且当x≥0时,f(x)=$\left\{\begin{array}{l}{{x}^{2}-1,0≤x<1}\\{lnx,x≥1}\end{array}\right.$,若对任意的x∈[a,a+1],不等式f(2x)≤f(x+a)恒成立,则实数a的最大值为( )| A. | -1 | B. | -$\frac{2}{3}$ | C. | -$\frac{1}{2}$ | D. | -$\frac{3}{4}$ |
分析 分析当x≥0时,结合二次函数和对数函数单调性可得f(x)的单调性,由偶函数的性质可得f(x)=f(|x|),
不等式f(2x)≤f(x+a)即为f(|2x|)≤f(|x+a|),即有|2x|≤|x+a|,结合二次函数的图象和不等式恒成立思想,解不等式即可得到所求最大值.
解答 解:当x≥0时,f(x)=$\left\{\begin{array}{l}{{x}^{2}-1,0≤x<1}\\{lnx,x≥1}\end{array}\right.$,
当x∈[0,1),y=x2-1递增,
且x=1,y=0,
当x≥1时,y=lnx递增,且经过点(1,0),
则有f(x)在[0,+∞)递增,
由偶函数的性质可得f(x)=f(|x|),
不等式f(2x)≤f(x+a)即为f(|2x|)≤f(|x+a|),
即有|2x|≤|x+a|,
即为(3x+a)(x-a)≤0,
对任意的x∈[a,a+1],不等式f(2x)≤f(x+a)恒成立,
由二次函数的图象可得,
(3a+a)(a-a)≤0,且[3(a+1)+a](a+1-a)≤0,
即为0≤0且a≤-$\frac{3}{4}$,
则有a≤-$\frac{3}{4}$.
a的最大值为-$\frac{3}{4}$.
故选:D.
点评 本题考查函数的奇偶性的判断和单调性的运用:解不等式,运用偶函数的性质和二次函数的图象是解题的关键,属于中档题和易错题.

练习册系列答案
相关题目
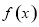 在
在 上是增函数,则满足
上是增函数,则满足 的实数
的实数 的取值范围是______________.
的取值范围是______________.