题目内容
4.设数列{an}:1,-2,-2,3,3,3,-4,-4,-4,-4,…,$\stackrel{k个}{\overbrace{(-1)^{k-1}k,…,(-1)^{k-1}k}}$,…,即当$\frac{(k-1)k}{2}$<n≤$\frac{k(k+1)}{2}$(k∈N*)时,${a}_{n}={(-1)}^{k-1}k$.记Sn=a1+a2+…+an(n∈N?).对于l∈N?,定义集合Pl=﹛n|Sn为an的整数倍,n∈N?,且1≤n≤l}(1)求P11中元素个数;
(2)求集合P2000中元素个数.
分析 (1)由数列{an}的定义,可得前11项,进而得到前11项和,再由定义集合Pl,即可得到元素个数;
(2)运用数学归纳法证明Si(2i+1)=-i(2i+1)(i∈N*).再结合定义,运用等差数列的求和公式,即可得到所求.
解答 解:(1)由数列{an}的定义得a1=1,a2=-2,a3=-2,a4=3,
a5=3,a6=3,a7=-4,a8=-4,a9=-4,a10=-4,a11=5,
所以S1=1,S2=-1,S3=-3,S4=0,S5=3,S6=6,S7=2,
S8=-2,S9=-6,S10=-10,S11=-5,
从而S1=a1,S4=0•a4,S5=a5,S6=2a6,S11=-a11,
所以集合P11中元素的个数为5;
(2)先证:Si(2i+1)=-i(2i+1)(i∈N*).
事实上,①当i=1时,Si(2i+1)=S3=-3,-i(2i+1)=-3,故原等式成立;
②假设i=m时成立,即Sm(2m+1)=-m(2m+1),则i=m+1时,
S(m+1)(2m+3)=Sm(2m+1)+(2m+1)2-(2m+2)2=-m(2m+1)-4m-3
=-(2m2+5m+3)=-(m+1)(2m+3).
综合①②可得Si(2i+1)=-i(2i+1).于是S(i+1)(2i+1)=Si(2i+1)+(2i+1)2
=-i(2i+1)+(2i+1)2=(2i+1)(i+1).
由上可知Si(2i+1)是2i+1的倍数,而ai(2i+1)+j=2i+1(j=1,2,…,2i+1),
所以Si(2i+1)+j=Si(2i+1)+j(2i+1)是ai(2i+1)+j(j=1,2,…,2i+1)的倍数.
又S(i+1)(2i+1)=(i+1)•(2i+1)不是2i+2的倍数,
而a(i+1)(2i+1)+j=-(2i+2)(j=1,2,…,2i+2),
所以S(i+1)(2i+1)+j=S(i+1)(2i+1)-j(2i+2)=(2i+1)(i+1)-j(2i+2)
不是a(i+1)(2i+1)+j(j=1,2,…,2i+2)的倍数,
故当l=i(2i+1)时,集合Pl中元素的个数为1+3+…+(2i-1)=i2,
于是,当l=i(2i+1)+j(1≤j≤2i+1)时,集合Pl中元素的个数为i2+j.
又2000=31×(2×31+1)+47,
故集合P2 000中元素的个数为312+47=1008.
点评 本题考查集合、数列的概念和运算、计数原理等基础知识,考查探究能力,以及运用数学归纳法的推理论证能力,有一定的难度.

| A. | ($\frac{3}{5}$,-$\frac{4}{5}$) | B. | (-$\frac{3}{5}$,$\frac{4}{5}$) | C. | ($\frac{3}{5}$,-$\frac{4}{5}$)或(-$\frac{3}{5}$,$\frac{4}{5}$) | D. | ($\frac{4}{5}$,-$\frac{3}{5}$)或(-$\frac{4}{5}$,$\frac{3}{5}$) |
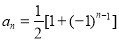

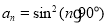
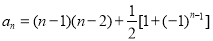
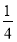 圆弧)( )
圆弧)( )
 B.
B.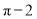
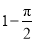 D.
D.