题目内容
16.高一新生军训时,经过两天的打靶训练,甲每射击10次可以击中9次,乙每射击9次可以击中8次.甲、乙两人射击同一目标(甲、乙两人互不影响),现各射击一次,目标被击中的概率为( )| A. | $\frac{9}{10}$ | B. | $\frac{4}{5}$ | C. | $\frac{8}{9}$ | D. | $\frac{89}{90}$ |
分析 先由题意根据独立事件的概率乘法公式求得两人都击不中的概率,再用1减去此概率,即为目标被击中的概率.
解答 解:由题意可得,甲射中的概率为$\frac{9}{10}$,乙射中的概率为$\frac{8}{9}$,
故两人都击不中的概率为(1-$\frac{9}{10}$)•(1-$\frac{8}{9}$)=$\frac{1}{90}$,
故目标被击中的概率为1-$\frac{1}{90}$=$\frac{89}{90}$,
故选:D.
点评 本题主要考查相互独立事件的概率乘法公式,所求的事件的概率与它的对立事件的概率之间的关系,属于基础题.

练习册系列答案
相关题目
6.已知函数f(x)=cos(2x+φ)(φ为常数)为奇函数,那么cosφ=( )
| A. | -$\frac{{\sqrt{2}}}{2}$ | B. | 0 | C. | $\frac{{\sqrt{2}}}{2}$ | D. | 1 |
7.如图所示程序框图中,输出S=( )
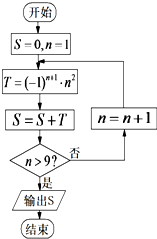

| A. | 45 | B. | 66 | C. | -66 | D. | -55 |
4.某军区新兵50m步枪射击个人平均成绩x(单位:环)服从正态分布N(μ,o2),从这些个人平均成绩中随机抽取100个,得到如下频数分布表:
(Ⅰ)求μ和o2的值(用样本数学期望、方差代替总体数学期望、方差);
(Ⅱ)如果这个军区有新兵10000名,试估计这个军区新兵50m步枪射击个人平均成绩在区间(7.9,8.8]上的人数[参考数据:$\sqrt{0.8}$=0.9,若ξ:N(μ,o2),则P(μ-o-<ξ≤μ+o-)=0.6826,P(μ-2o-<ξ≤μ+2o-)=0.9544,P(μ-3o-<ξ≤μ+3o-=0.9974].
| x | 4 | 5 | 6 | 7 | 8 | 9 |
| 频数 | 1 | 2 | 26 | 40 | 29 | 2 |
(Ⅱ)如果这个军区有新兵10000名,试估计这个军区新兵50m步枪射击个人平均成绩在区间(7.9,8.8]上的人数[参考数据:$\sqrt{0.8}$=0.9,若ξ:N(μ,o2),则P(μ-o-<ξ≤μ+o-)=0.6826,P(μ-2o-<ξ≤μ+2o-)=0.9544,P(μ-3o-<ξ≤μ+3o-=0.9974].
3.已知集合A={-1,0,1,2},集合B={x∈R|x2=1},则A∩B=( )
| A. | {1} | B. | {-1,1} | C. | {-1,0,1} | D. | {-1,0,1,2} |
4.已知集合M={x|0<x<3},N={x|log2x>1},则M∩N=( )
| A. | ∅ | B. | {x|0<x<3} | C. | {x|1<x<3} | D. | {x|2<x<3} |
 已知函数$y=sin(ωx+φ)(ω>0,0<φ≤\frac{π}{2})$的部分图象如图所示.
已知函数$y=sin(ωx+φ)(ω>0,0<φ≤\frac{π}{2})$的部分图象如图所示.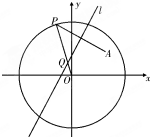 如图,已知点A为圆x2+y2=16内一定点,P是圆上任意一点,线段AP的垂直平分线l和半径OP相交于点Q,当点P在圆上运动时,点Q的轨迹是( )
如图,已知点A为圆x2+y2=16内一定点,P是圆上任意一点,线段AP的垂直平分线l和半径OP相交于点Q,当点P在圆上运动时,点Q的轨迹是( )