题目内容
15.设四边形ABCD为平行四边形,|$\overrightarrow{AB}$|=6,|$\overrightarrow{AD}$|=4,则$\overrightarrow{AC}•\overrightarrow{DB}$=( )| A. | 10 | B. | 15 | C. | 20 | D. | 25 |
分析 根据平面向量的平行四边形法则将所求利用$\overrightarrow{AB}$,$\overrightarrow{AD}$表示,然后展开计算.
解答 解:因为四边形ABCD为平行四边形,|$\overrightarrow{AB}$|=6,|$\overrightarrow{AD}$|=4,则$\overrightarrow{AC}•\overrightarrow{DB}$=($\overrightarrow{AB}+\overrightarrow{AD}$)($\overrightarrow{AB}-\overrightarrow{AD}$)=${\overrightarrow{AB}}^{2}-{\overrightarrow{AD}}^{2}$=62-42=20;
故选:C.
点评 本题考查了向量的平行四边形法则以及数量积的计算;关键是将所求利用$\overrightarrow{AB}$,$\overrightarrow{AD}$表示.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6.已知函数f(x)=cos(2x+φ)(φ为常数)为奇函数,那么cosφ=( )
| A. | -$\frac{{\sqrt{2}}}{2}$ | B. | 0 | C. | $\frac{{\sqrt{2}}}{2}$ | D. | 1 |
7.如图所示程序框图中,输出S=( )
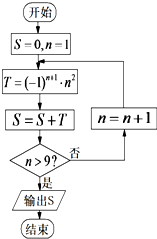

| A. | 45 | B. | 66 | C. | -66 | D. | -55 |
4.某军区新兵50m步枪射击个人平均成绩x(单位:环)服从正态分布N(μ,o2),从这些个人平均成绩中随机抽取100个,得到如下频数分布表:
(Ⅰ)求μ和o2的值(用样本数学期望、方差代替总体数学期望、方差);
(Ⅱ)如果这个军区有新兵10000名,试估计这个军区新兵50m步枪射击个人平均成绩在区间(7.9,8.8]上的人数[参考数据:$\sqrt{0.8}$=0.9,若ξ:N(μ,o2),则P(μ-o-<ξ≤μ+o-)=0.6826,P(μ-2o-<ξ≤μ+2o-)=0.9544,P(μ-3o-<ξ≤μ+3o-=0.9974].
| x | 4 | 5 | 6 | 7 | 8 | 9 |
| 频数 | 1 | 2 | 26 | 40 | 29 | 2 |
(Ⅱ)如果这个军区有新兵10000名,试估计这个军区新兵50m步枪射击个人平均成绩在区间(7.9,8.8]上的人数[参考数据:$\sqrt{0.8}$=0.9,若ξ:N(μ,o2),则P(μ-o-<ξ≤μ+o-)=0.6826,P(μ-2o-<ξ≤μ+2o-)=0.9544,P(μ-3o-<ξ≤μ+3o-=0.9974].
3.已知集合A={-1,0,1,2},集合B={x∈R|x2=1},则A∩B=( )
| A. | {1} | B. | {-1,1} | C. | {-1,0,1} | D. | {-1,0,1,2} |
 如图,在直角坐标系中,曲线段AB是函数y=1-x2图象的一部分,P为曲线段AB上异于点A,B一个动点,PM丄x轴,垂足为M,PN丄y轴,垂足为N.
如图,在直角坐标系中,曲线段AB是函数y=1-x2图象的一部分,P为曲线段AB上异于点A,B一个动点,PM丄x轴,垂足为M,PN丄y轴,垂足为N.