题目内容
15.已知数列{an}中,an=$\left\{\begin{array}{l}{{2}^{n-1}(n为正奇数)}\\{2n-1(n为正偶数)}\end{array}\right.$,设数列{an}的前n项和为Sn,则S9=377.(用数字作答).分析 根据数列的通项公式进行求解即可.
解答 解:S9=(20+22+24+26+28)+(3+7+11+15)
=$\frac{1-{4}^{5}}{1-4}$+36
=341+36=377,
故答案为:377
点评 本题主要考查数列求和,结合等差数列和等比数列的通项公式是解决本题的关键.

练习册系列答案
相关题目
7.如图所示程序框图中,输出S=( )
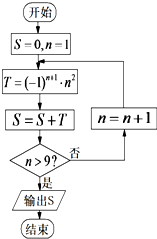

| A. | 45 | B. | 66 | C. | -66 | D. | -55 |
3.已知集合A={-1,0,1,2},集合B={x∈R|x2=1},则A∩B=( )
| A. | {1} | B. | {-1,1} | C. | {-1,0,1} | D. | {-1,0,1,2} |
7.如图所示,平面内z1,z2对应的向量分别是$\overrightarrow{OA}$,$\overrightarrow{OB}$,则|z1+z2|=( )
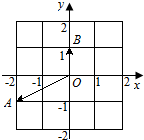

| A. | 2 | B. | 3 | C. | 2 $\sqrt{2}$ | D. | 3 $\sqrt{3}$ |
4.已知集合M={x|0<x<3},N={x|log2x>1},则M∩N=( )
| A. | ∅ | B. | {x|0<x<3} | C. | {x|1<x<3} | D. | {x|2<x<3} |
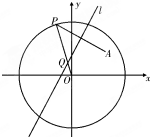 如图,已知点A为圆x2+y2=16内一定点,P是圆上任意一点,线段AP的垂直平分线l和半径OP相交于点Q,当点P在圆上运动时,点Q的轨迹是( )
如图,已知点A为圆x2+y2=16内一定点,P是圆上任意一点,线段AP的垂直平分线l和半径OP相交于点Q,当点P在圆上运动时,点Q的轨迹是( )