题目内容
2．不等式$\frac{2x-1}{x+1}＞1$的解集为{x|x＜-1，或 x＞2}．分析 把要解的不等式等价转化为（x-2）（x+1）＞0，从而求得它的解集．
解答 解：不等式$\frac{2x-1}{x+1}＞1$，即 $\frac{x-2}{x+1}$＞0，即 （x-2）（x+1）＞0．
求得它的解集为{x|x＜-1，或 x＞2}，
故答案为：{x|x＜-1，或 x＞2}．
点评 本题主要考查分式不等式的解法，一元二次不等式的解法，体现了等价转化的数学思想，属于基础题．
练习册系列答案
能力评价系列答案
唐印文化课时测评系列答案
相关题目
12．复数$1+\frac{5}{2-i}$（i是虚数单位）的模等于（ ）
| A． | $\sqrt{10}$ | B． | 10 | C． | $\sqrt{5}$ | D． | 5 |
13．圆C：x2+y2+4x-2y+3=0的圆心坐标及半径分别是（ ）
| A． | （-2，1），$\sqrt{2}$ | B． | （2，1），$\sqrt{2}$ | C． | （-2，1），2 | D． | （2，-1），2 |
17．已知α是第二象限角，sinα=$\frac{5}{13}$，则cosα=（ ）
| A． | -$\frac{5}{13}$ | B． | -$\frac{12}{13}$ | C． | $\frac{5}{13}$ | D． | $\frac{12}{13}$ |
7．如图所示程序框图中，输出S=（ ）
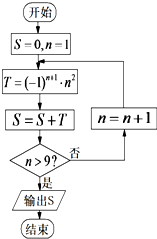
| A． | 45 | B． | 66 | C． | -66 | D． | -55 |
14．已知函数y=2x2-2x+1的导数为y′，y′=（ ）
| A． | 2x-2 | B． | 4x+1 | C． | 4x-2 | D． | 2x+1 |
已知函数$y=sin（ωx+φ）（ω＞0，0＜φ≤\frac{π}{2}）$的部分图象如图所示．