题目内容
【题目】已知f（x）是定义在（0，+∞）上的增函数，且满足f（xy）=f（x）+f（y），f（2）=1．
（1）求f（4）与f（8）的值；
（2）解不等式f（x）﹣f（x﹣2）＞3．
【答案】
（1）解：∵f（xy）=f（x）+f（y），f（2）=1．
∴f（4）=f（2×2）=f（2）+f（2）=2
∴f（8）=f（4×2）=f（4）+f（2）=3
（2）解：根据题意，不等式f（x）﹣f（x﹣2）＞3可变为
f（x）＞f（x﹣2）+3=f（x﹣2）+f（8）=f[8（x﹣2）]
∵f（x）在（0，+∞）上是增函数，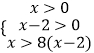 
，
解得 
，
∴原不等式的解集是 
【解析】（1）直接把4分成2×2，再代入f（xy）=f（x）+f（y），结合f（2）=1即可求出f（4）的值，同理可得f（8）的值；（2）先把不等式f（x）﹣f（x﹣2）＞3转化为f（x）＞f（x﹣2）+3=f（x﹣2）+f（8）=f[8（x﹣2）]；再结合f（x）是定义在（0，+∞）上的增函数即可求出不等式的解集．（注意其定义域的限制）
练习册系列答案
名校课堂系列答案
相关题目
