题目内容
19.设函数f(x)=$\sqrt{3}+\frac{sinx}{1+cosx}$的所有正的零点从小到大依次为x1,x2,x3,…,设α=x1+x2+x3+…+x2015,则sinα的值是( )| A. | 0 | B. | -$\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | 1 |
分析 由条件可得sinx+cosx=-1,且1+cosx≠0,求得x=2kπ+$\frac{4π}{3}$,k∈z;从而求得α=x1+x2+x3+…+x2015的值;再利用诱导公式求得sinα的值.
解答 解:令函数f(x)=$\sqrt{3}+\frac{sinx}{1+cosx}$=0,求得2sin(x+$\frac{π}{3}$)=-$\sqrt{3}$,且1+cosx≠0,
∴sin(x+$\frac{π}{3}$)=-$\frac{\sqrt{3}}{2}$,且1+cosx≠0,
∴x+$\frac{π}{3}$=2kπ+$\frac{4π}{3}$,k∈z.或x+$\frac{π}{3}$=2kπ+$\frac{5π}{3}$,k∈z.且x≠2kπ+π,k∈Z.
可得:x=2kπ+π,k∈Z(矛盾,舍去)或x=2kπ+$\frac{4π}{3}$,k∈Z,
由题意可得x1 =$\frac{4π}{3}$,x2 =2π+$\frac{4π}{3}$,x3 =4π+$\frac{4π}{3}$…,x2015 =2014×2π+$\frac{4π}{3}$,
∴α=x1+x2+x3+…+x2015=(1+2+3+…+2014)2π+2015×$\frac{4π}{3}$,
∴sinα=sin(2015×$\frac{4π}{3}$)=sin(2686π+$\frac{2π}{3}$)=sin$\frac{2π}{3}$=$\frac{\sqrt{3}}{2}$,
故选:C.
点评 本题主要考查函数零点的定义,同角三角函数的基本关系、诱导公式的应用,属于基础题.

练习册系列答案
相关题目
11.二次函数f(x)=ax2+bx+c(a>0)的图象与x轴交点的横坐标为-5和3,则这个二次函数的单调减区间为( )
| A. | (-∞,-1] | B. | [2,+∞) | C. | (-∞,2] | D. | [-1,+∞) |
14.设定义在(1,e)上的函数f(x)=$\sqrt{lnx+4x-a}$(a∈R),若曲线y=1+sinx上存在(x0,y0)使得f(f(y0))=y0,则a的取值范围( )
| A. | (-∞,4+ln2] | B. | (3,4] | C. | (3,4+ln2] | D. | (2,ln2] |
9.若实数a,b,c,d满足(b+2a2-6lna)2+|2c-d+6|=0,(a-c)2+(b-d)2的最小值为m,则函数f(x)=ex+$\frac{1}{5}$mx-3零点所在的区间为( )
| A. | $({-\frac{1}{4},0})$ | B. | $({0,\frac{1}{4}})$ | C. | $({\frac{1}{4},\frac{1}{2}})$ | D. | $({\frac{1}{2},1})$ |
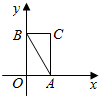 已知椭圆C的方程为$\frac{{x}^{2}}{{m}^{2}}$+$\frac{{y}^{2}}{4{m}^{2}}$=1(m>0),如图所示,在平面直角坐标系xOy中,△ABC的三个顶点的坐标分别为A(1,0),B(0,2),C(1,2)
已知椭圆C的方程为$\frac{{x}^{2}}{{m}^{2}}$+$\frac{{y}^{2}}{4{m}^{2}}$=1(m>0),如图所示,在平面直角坐标系xOy中,△ABC的三个顶点的坐标分别为A(1,0),B(0,2),C(1,2)