题目内容
4.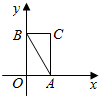 已知椭圆C的方程为$\frac{{x}^{2}}{{m}^{2}}$+$\frac{{y}^{2}}{4{m}^{2}}$=1(m>0),如图所示,在平面直角坐标系xOy中,△ABC的三个顶点的坐标分别为A(1,0),B(0,2),C(1,2)
已知椭圆C的方程为$\frac{{x}^{2}}{{m}^{2}}$+$\frac{{y}^{2}}{4{m}^{2}}$=1(m>0),如图所示,在平面直角坐标系xOy中,△ABC的三个顶点的坐标分别为A(1,0),B(0,2),C(1,2)(Ⅰ)当椭圆C与直线AB相切时,求m的值;
(Ⅱ)若椭圆C与△ABC三边无公共点,求m的取值范围;
(Ⅲ)若椭圆C与△ABC三边相交于不同的两点M,N,求△OMN的面积S的最大值.
分析 (Ⅰ)求得直线AB的方程,联立椭圆方程,由判别式为0,计算即可得到m的值;
(Ⅱ)由图可知当椭圆C在直线AB的左下方或△ABC在椭圆内时,两者便无公共点.通过判别式小于0,或C在椭圆内,解不等式即可得到所求范围;
(Ⅲ)对m讨论,①当$\frac{\sqrt{2}}{2}$<m≤1时,M,N在线段AB上,②当1<m≤$\sqrt{2}$时,点M,N分别在线段BC,AC上,求得△OMN的面积,化简整理可得S的最大值.
解答 解:(Ⅰ)直线AB的方程:y=-2x+2,
联立$\left\{\begin{array}{l}{y=2-2x}\\{4{x}^{2}+{y}^{2}=4{m}^{2}}\end{array}\right.$,消去y得2x2-2x+1-m2=0,
由△=4-8(1-m2)=0 得m2=$\frac{1}{2}$,
又m>0,即有m=$\frac{\sqrt{2}}{2}$,
(Ⅱ)由图可知当椭圆C在直线AB的左下方或△ABC在椭圆内时,
两者便无公共点.
①当椭圆C在直线AB的左下方时,
△=4-8(1-m2)<0 解得0<m<$\frac{\sqrt{2}}{2}$;
②当且当点C(1,2)在椭圆内时,△ABC在椭圆内,
$\frac{1}{{m}^{2}}$+$\frac{4}{{m}^{2}}$<1 又m>0,m>$\sqrt{2}$,
综上所述,当0<m<$\frac{\sqrt{2}}{2}$或m>$\sqrt{2}$时,椭圆与C无公共点;
(Ⅲ)由(Ⅱ)可知当$\frac{\sqrt{2}}{2}$<m<$\sqrt{2}$时,椭圆C与△ABC相交于不同的两个点M,N,
又因为当m=1时,椭圆C方程为x2+$\frac{{y}^{2}}{4}$=1,此时椭圆恰好过点A,B,
①当$\frac{\sqrt{2}}{2}$<m≤1时,M,N在线段AB上,此时S≤S△ABC=1,
当且仅当M,N分别与A,B重合时等号成立;
②当1<m≤$\sqrt{2}$时,点M,N分别在线段BC,AC上,易得M($\sqrt{{m}^{2}-1}$,2),N(1,2$\sqrt{{m}^{2}-1}$)
S=S矩形OACB-S△OBM-S△OAN-S△MNC
=2-$\sqrt{{m}^{2}-1}$-$\sqrt{{m}^{2}-1}$-$\frac{1}{2}$(1-$\sqrt{{m}^{2}-1}$)(2-2$\sqrt{{m}^{2}-1}$)
=2-2$\sqrt{{m}^{2}-1}$-(1-$\sqrt{{m}^{2}-1}$)2,
令t=$\sqrt{{m}^{2}-1}$,则0<t<1,S=-t2+1<1,
综上可得△OMN面积S的最大值为1.
点评 本题考查椭圆的方程和性质,主要考查椭圆与直线相切、相交的位置关系,通过椭圆的变化研究与三角形的位置关系是解题的关键.

 孟建平名校考卷系列答案
孟建平名校考卷系列答案| A. | 0 | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | 1 |
| A. | 0 | B. | -$\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | 1 |
| A. | 2+π | B. | 2+$\frac{π}{2}$ | C. | 4+2π | D. | 4+4π |
| A. | 5,10,15,20 | B. | 2,12,22,32 | C. | 2,14,26,38 | D. | 5,8,31,36 |
| A. | 5 | B. | $2\sqrt{5}$ | C. | 20 | D. | 4$\sqrt{5}$ |
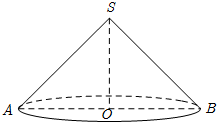 如图,已知圆锥的轴截面SAB是等腰直角三角形,且该圆锥体积为$\frac{8}{3}$π,求该圆锥的表面积.
如图,已知圆锥的轴截面SAB是等腰直角三角形,且该圆锥体积为$\frac{8}{3}$π,求该圆锥的表面积.