题目内容
7.已知椭圆4x2+y2=1及直线y=x+m,求直线被椭圆截得的线段AB最长时的直线方程.分析 设直线与椭圆的公共点为A(x1,y1),B(x2,y2),表示出|AB|,变形后利用韦达定理表示出两根之和与两根之积,代入化简,利用二次函数的性质求出|AB|最大值,以及此时m的值,即可确定出此时直线l的方程.
解答 解:联立得:$\left\{\begin{array}{l}{4{x}^{2}+{y}^{2}=1}\\{y=x+m}\end{array}\right.$,
消去y得:5x2+2mx+m2-1=0,
由△=-16m2+20≥0,得-$\frac{\sqrt{5}}{2}$≤m≤$\frac{\sqrt{5}}{2}$,
设直线与椭圆的公共点为A(x1,y1),B(x2,y2),
则|AB|=$\sqrt{1+{k}^{2}}$|x1-x2|=$\sqrt{2}$$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\frac{2\sqrt{2}}{5}$$\sqrt{5-4{m}^{2}}$,
∵m∈[-$\frac{\sqrt{5}}{2}$,$\frac{\sqrt{5}}{2}$],
∴当m=0时,|AB|max=$\frac{2\sqrt{10}}{5}$,此时直线l:y=x.
点评 本题考查了直线与椭圆的位置关系;关键是利用弦长公式得到关于m的式子,利用m的范围求弦长最值.

练习册系列答案
相关题目
19.设函数f(x)=$\sqrt{3}+\frac{sinx}{1+cosx}$的所有正的零点从小到大依次为x1,x2,x3,…,设α=x1+x2+x3+…+x2015,则sinα的值是( )
| A. | 0 | B. | -$\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | 1 |
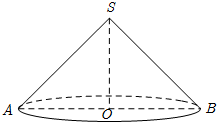 如图,已知圆锥的轴截面SAB是等腰直角三角形,且该圆锥体积为$\frac{8}{3}$π,求该圆锥的表面积.
如图,已知圆锥的轴截面SAB是等腰直角三角形,且该圆锥体积为$\frac{8}{3}$π,求该圆锥的表面积.