题目内容
设f(x)是定义在R上的增函数,且对于任意的x都有f(1-x)+f(1+x)=0恒成立.如果实数m、n满足不等式组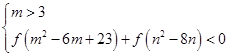 那么m2+n2的取值范围是________.
那么m2+n2的取值范围是________.
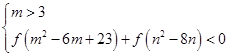 那么m2+n2的取值范围是________.
那么m2+n2的取值范围是________.(13,49)
由f(1-x)+f(1+x)=0得,f(n2-8n)=f[(n2-8n-1)+1]=-f[1-(n2-8n-1)]=-f(-n2+8n+2),所以f(m2-6m+23)<-f(n2-8n)=f(-n2+8n+2),又f(x)是定义在R上的增函数,所以m2-6m+23<-n2+8n+2,即为(m-3)2+(n-4)2<4,且m>3,所以(m,n)在以(3,4)为圆心,半径为2的右半个圆内,当为点(3,2)时,m2+n2=13,圆心(3,4)到原点的距离为5,此时
m2+n2=(5+2)2=49,所以m2+n2的取值范围是(13,49).
m2+n2=(5+2)2=49,所以m2+n2的取值范围是(13,49).

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
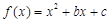 ,其中
,其中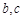 为常数.
为常数. 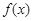 在区间
在区间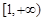 上单调,求
上单调,求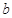 的取值范围;
的取值范围;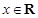 ,都有
,都有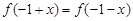 成立,且函数
成立,且函数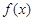 的图象经过点
的图象经过点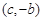 ,
,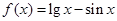 ,则
,则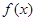 在
在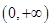 上的零点个数为( )
上的零点个数为( )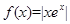 ,关于
,关于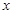 的方程
的方程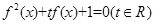 有四个不等实数根,则
有四个不等实数根,则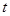 的取值范围为( )
的取值范围为( )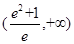
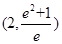

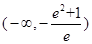
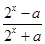 在其定义域上为奇函数”的________条件.(填“充分不必要”“必要不充分”“充要”“既不充分也不必要”)
在其定义域上为奇函数”的________条件.(填“充分不必要”“必要不充分”“充要”“既不充分也不必要”)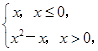 若函数g(x)=f(x)-m有三个不同的零点,则实数m的取值范围为( )
若函数g(x)=f(x)-m有三个不同的零点,则实数m的取值范围为( ) 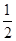 ,1
,1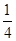 ,0
,0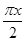 ;④f(x)=ln x+1.其中存在稳定区间的函数有________(写出所有正确命题的序号).
;④f(x)=ln x+1.其中存在稳定区间的函数有________(写出所有正确命题的序号).