题目内容
已知函数f(x)=2|x-2|+ax(x∈R)有最小值.
(1)求实数a的取值范围.
(2)设g(x)为定义在R上的奇函数,且当x<0时,g(x)=f(x),求g(x)的解析式.
(1)求实数a的取值范围.
(2)设g(x)为定义在R上的奇函数,且当x<0时,g(x)=f(x),求g(x)的解析式.
(1) [-2,2] (2)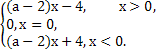
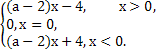
(1)f(x)=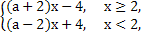
要使函数f(x)有最小值,需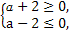 ∴-2≤a≤2,
∴-2≤a≤2,
即当a∈[-2,2]时,f(x)有最小值.
(2)∵g(x)为定义在R上的奇函数,∴g(0)=0.
设x>0,则-x<0,
∴g(x)=-g(-x)=(a-2)x-4,
∴g(x)=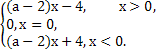
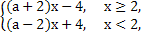
要使函数f(x)有最小值,需
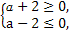 ∴-2≤a≤2,
∴-2≤a≤2,即当a∈[-2,2]时,f(x)有最小值.
(2)∵g(x)为定义在R上的奇函数,∴g(0)=0.
设x>0,则-x<0,
∴g(x)=-g(-x)=(a-2)x-4,
∴g(x)=
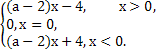

练习册系列答案
相关题目
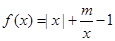
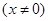 .
. 时,判断
时,判断 在
在 的单调性,并用定义证明.
的单调性,并用定义证明. ,不等式
,不等式 恒成立,求
恒成立,求 的取值范围;
的取值范围;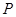 和
和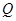 (万元),它们与投入资金
(万元),它们与投入资金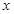 (万元)的关系依次是:其中
(万元)的关系依次是:其中 的图像过点
的图像过点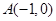 和
和 ,则下列各点在函数
,则下列各点在函数

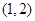

 ,对任意x∈[1,+∞),f(2mx)+2mf(x)<0恒成立,则实数m的取值范围是________.
,对任意x∈[1,+∞),f(2mx)+2mf(x)<0恒成立,则实数m的取值范围是________. ,则当x∈(-∞,-2)时,f(x)的解析式为( )
,则当x∈(-∞,-2)时,f(x)的解析式为( )


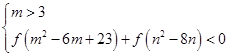 那么m2+n2的取值范围是________.
那么m2+n2的取值范围是________.