题目内容
已知函数f(x)＝m－|x－2|，m∈R，且f(x＋2)≥0的解集为[－1，1]．
(1)求m的值；
(2)若a，b，c∈R，且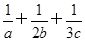
＝m，求证：a＋2b＋3c≥9.
(1)求m的值；
(2)若a，b，c∈R，且
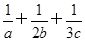＝m，求证：a＋2b＋3c≥9.（1）m＝1（2）见解析
(1)∵f(x＋2)＝m－|x|≥0，∴|x|≤m，∴m≥0，－m≤x≤m，
∴f(x＋2)≥0的解集是[－1，1]，故m＝1.
(2)由(1)知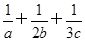＝1，a、b、c∈R，由柯西不等式得a＋2b＋3c＝(a＋2b＋3c)
≥(
·
＋
·
＋
·
)2＝9.
∴f(x＋2)≥0的解集是[－1，1]，故m＝1.
(2)由(1)知
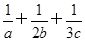＝1，a、b、c∈R，由柯西不等式得a＋2b＋3c＝(a＋2b＋3c)≥(·＋·＋·)2＝9.
练习册系列答案
鹰派教辅衔接教材河北教育出版社系列答案
相关题目
≥1”的 ( )
≤k恒成立，求k的取值范围．
与
的大小．
，
的值域为_________.