题目内容
已知m∈R,设命题P:-3≤m-5≤3;命题Q:函数f(x)=3x2+2mx+m+
有两个不同的零点.求使命题“P或Q”为真命题的实数m的取值范围.
| 4 |
| 3 |
∵-3≤m-5≤3,∴2≤m≤8,
即P:2≤m≤8.
∵函数f(x)=3x2+2mx+m+
有两个不同的零点,
∴判别式△>0,即△=4m2-12(m+
)=4m2-12m-16>0,
∴m2-3m-4>0,解得m>4或m<-1,
即Q:m>4或m<-1.
∵“P或Q”为真命题,
∴P,Q至少有一个为真命题.
当P,Q同时为假命题时,
满足
,解得-1≤m<2,
∴P,Q至少有一个为真命题时,
满足m≥2或m<-1.
即实数m的取值范围是m≥2或m<-1.
即P:2≤m≤8.
∵函数f(x)=3x2+2mx+m+
| 4 |
| 3 |
∴判别式△>0,即△=4m2-12(m+
| 4 |
| 3 |
∴m2-3m-4>0,解得m>4或m<-1,
即Q:m>4或m<-1.
∵“P或Q”为真命题,
∴P,Q至少有一个为真命题.
当P,Q同时为假命题时,
满足
|
∴P,Q至少有一个为真命题时,
满足m≥2或m<-1.
即实数m的取值范围是m≥2或m<-1.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
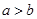 成立的充分而不必要的条件是( )
成立的充分而不必要的条件是( )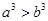
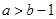
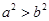
 .
.