题目内容
已知m∈R,设条件p:不等式(m2-1)x2+(m+1)x+1≥0对任意的x∈R恒成立;条件q:关于x的不等式|x+1|+|x-2|<m的解集为Φ.
(1)分别求出使得p以及q为真的m的取值范围;
(2)若复合命题“p或q”为真,“p且q”为假,求实数m的取值范围.
(1)分别求出使得p以及q为真的m的取值范围;
(2)若复合命题“p或q”为真,“p且q”为假,求实数m的取值范围.
(1)∵p:不等式(m2-1)x2+(m+1)x+1≥0对任意的x∈R恒成立
当p为真时,
∴m=-1或
?m≤-1或m≥
又∵q:关于x的不等式|x+1|+|x-2|<m的解集为Φ
当q为真,
∴(|x+1|+|x-2|)min≥m?m≤3,
∴p真时m的取值范围为A={m|m≤-1或m≥
},q真时m的取值范围为B={m|m≤3};
(2)∵“p或q”为真,“p且q”为假,
∴p和q一真一假,分两况讨论:
1°当p真且q假时,有A∩CRB={m|m>3};
2°当p假且q真时,有(CRA)∩B={m|-1<m<
},
1°,2°取并,
即得“p或q”为真,“p且q”为假时实数m的取值范围是{m|-1<m<
或m>3}
当p为真时,
∴m=-1或
|
| 5 |
| 3 |
又∵q:关于x的不等式|x+1|+|x-2|<m的解集为Φ
当q为真,
∴(|x+1|+|x-2|)min≥m?m≤3,
∴p真时m的取值范围为A={m|m≤-1或m≥
| 5 |
| 3 |
(2)∵“p或q”为真,“p且q”为假,
∴p和q一真一假,分两况讨论:
1°当p真且q假时,有A∩CRB={m|m>3};
2°当p假且q真时,有(CRA)∩B={m|-1<m<
| 5 |
| 3 |
1°,2°取并,
即得“p或q”为真,“p且q”为假时实数m的取值范围是{m|-1<m<
| 5 |
| 3 |

练习册系列答案
相关题目
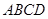 的两条对角线为
的两条对角线为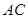 、
、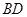 ,则“四边形
,则“四边形 ”的( )
”的( )