题目内容
13.函数f(x)在定义域R内可导,若f(x)=f(1-x),(x-$\frac{1}{2}$)f′(x)<0,设a=f(0),b=f($\frac{1}{2}$),c=f(3),则( )| A. | a<b<c | B. | c<a<b | C. | c<b<a | D. | b<c<a |
分析 由函数满足f(x)=f(1-x)知,f(x)关于x=$\frac{1}{2}$对称,又满足不等式)(x-$\frac{1}{2}$)f′(x)<0,得f(x)的单调性,利用单调性就可以比较a,b,c的大小.
解答 解:∵f(x)=f(1-x),∴函数f(x)的图象关于x=$\frac{1}{2}$对称,∴f(0)=f(1)
又∵(x-$\frac{1}{2}$)f′(x)<0,∴当$x∈(-∞,\frac{1}{2})$时,f′(x)>0,f(x)单调递增,
当$x∈(\frac{1}{2},+∞)时$,f′(x)<0,f(x)单调递减,
∵$\frac{1}{2}<1<3$
∴$f(\frac{1}{2})>f(1)>f(3)$
∴$f(\frac{1}{2})>f(0)>f(3)$,即b>a>c
故选B.
点评 本题利用函数的对称性,单调性比较函数值的大小,属于中档题.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
3.一个工厂为了规定工时定额,需要确定加工零件所花费的时间,为此进行了10次试验,收集数据如下:
(1)画出散点图;
(2)推出是正相关还是负相关;
(3)关于加工零件的个数与加工时间,你能得出什么结论?
| 零件数 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
| 加工时间 | 62 | 68 | 75 | 81 | 89 | 95 | 102 | 108 | 115 | 122 |
(2)推出是正相关还是负相关;
(3)关于加工零件的个数与加工时间,你能得出什么结论?
4.设x,y满足约束条件$\left\{\begin{array}{l}{x+y≥a}\\{x-y≤-1}\end{array}\right.$,且z=x+ay,则( )
| A. | 当a>0时有最大值 | B. | 当a>1时有最小值 | ||
| C. | 当a<0时有最大值 | D. | 当0<a<1时有最小值 |
8.(重点中学做)如图所示,程序框图输出的某一实数对(x,y)中,若y=1024,则x=( )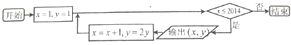
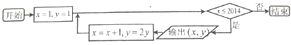
| A. | 9 | B. | 10 | C. | 11 | D. | 12 |