Question

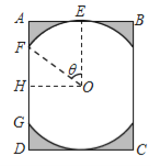
【题目】【苏北三市（连云港、徐州、宿迁）2017届高三年级第三次调研考试】某景区修建一栋复古建筑，其窗户设计如图所示.圆的圆心与矩形对角线的交点重合，且圆与矩形上下两边相切（为上切点），与左右两边相交（，为其中两个交点），图中阴影部分为不透光区域，其余部分为透光区域.已知圆的半径为1，且，设，透光区域的面积为.

（1）求关于的函数关系式，并求出定义域；

（2）根据设计要求，透光区域与矩形窗面的面积比值越大越好.当该比值最大时，求边的长度.

Answer 1

【答案】（1）关于的函数关系式为，定义域为；

（2）透光区域与矩形窗面的面积比值最大时，的长度为1．

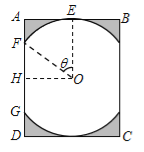
【解析】解:(1)过点作于点，则，

所以，

．

所以

，

因为，所以，所以定义域为．

（2）矩形窗面的面积为．

则透光区域与矩形窗面的面积比值为．

设，．

则

，

因为，所以，所以，故，

所以函数在上单调减．

所以当时，有最大值，此时

答：（1）关于的函数关系式为，定义域为；

（2）透光区域与矩形窗面的面积比值最大时，的长度为1．