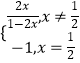题目内容
【题目】已知数列{an}的前n项和为Sn , 且Sn=2an﹣2(n∈N*),数列{bn}满足b1=1,且点P(bn , bn+1)(n∈N*)在直线y=x+2上.
(1)求数列{an}、{bn}的通项公式;
(2)求数列{anbn}的前n项和Dn;
(3)设cn=ansin2 ![]() ,求数列{cn}的前2n项和T2n .
,求数列{cn}的前2n项和T2n .
【答案】
(1)解:当n=1,a1=2
当n≥2时,an=Sn﹣Sn﹣1=2an﹣2an﹣1
∴an=2an﹣1(n≥2),∴{an}是等比数列,公比为2,首项a1=2
∴ ![]()
又点 ![]() 在直线y=x+2上,∴bn+1=bn+2,
在直线y=x+2上,∴bn+1=bn+2,
∴{bn}是等差数列,公差为2,首项b1=1,∴bn=2n﹣1
(2)解:∵ ![]()
∴ ![]() ①
①
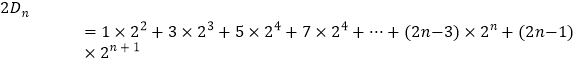 ②
②
①﹣②得 ![]()
= ![]()
![]()
(3)解: ![]()
T2n=(a1+a3+…+a2n﹣1)﹣(b2+b4+…b2n)
= ![]()
【解析】(1)利用数列递推式,再写一式,两式相减,可求求数列{an}的通项公式;利用点 ![]() 在直线y=x+2上,可得{bn}是等差数列,公差为2,首项b1=1,从而可求{bn}的通项公式;(2)利用错位相减法,可求数列{anbn}的前n项和Dn;(3)利用分组求和法,可求数列{cn}的前2n项和T2n .
在直线y=x+2上,可得{bn}是等差数列,公差为2,首项b1=1,从而可求{bn}的通项公式;(2)利用错位相减法,可求数列{anbn}的前n项和Dn;(3)利用分组求和法,可求数列{cn}的前2n项和T2n .
【考点精析】掌握数列的前n项和是解答本题的根本,需要知道数列{an}的前n项和sn与通项an的关系 .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目