题目内容
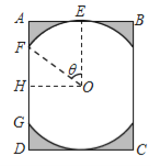
【题目】在平面直角坐标系xoy中，圆C的方程为x2+y2﹣8x+15=0，若直线y=kx+2上至少存在一点，使得以该点为圆心，半径为1的圆与圆C有公共点，则k的最小值是（ ）
A.-
B.-
C.-
D.-
【答案】A
【解析】∵圆C的方程为x2+y2﹣8x+15=0，整理得：（x﹣4）2+y2=1，即圆C是以（4，0）为圆心，1为半径的圆；
又直线y=kx+2上至少存在一点，使得以该点为圆心，1为半径的圆与圆C有公共点，
∴只需圆C′：（x﹣4）2+y2=4与直线y=kx+2有公共点即可．
设圆心C（4，0）到直线y=kx+2的距离为d，
则d=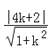
≤2，即3k2≤﹣4k，
∴﹣
≤k≤0．
∴k的最小值是- ．
故选A．
化圆C的方程为（x﹣4）2+y2=1，求出圆心与半径，由题意，只需（x﹣4）2+y2=4与直线y=kx+2有公共点即可．
练习册系列答案
阅读快车系列答案
相关题目
