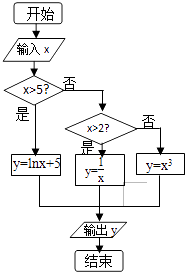
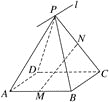
题目内容
【题目】已知函数f(x)=e﹣x(lnx﹣2k)(k为常数,e=2.71828…是自然对数的底数),曲线y=f(x)在点(1,f(1))处的切线与y轴垂直.
(1)求f(x)的单调区间;
(2)设 ![]() ,对任意x>0,证明:(x+1)g(x)<ex+ex﹣2 .
,对任意x>0,证明:(x+1)g(x)<ex+ex﹣2 .
【答案】
(1)解:因为 ![]() ,
,
由已知得 ![]() ,∴
,∴ ![]() .
.
所以 ![]() ,
,
设 ![]() ,则
,则 ![]() ,
,
在(0,+∞)上恒成立,即k(x)在(0,+∞)上是减函数,
由k(1)=0知,当0<x<1时k(x)>0,
从而f'(x)>0,当x>1时k(x)<0,从而f'(x)<0.
综上可知,f(x)的单调递增区间是(0,1),单调递减区间是(1,+∞)
(2)解:因为x>0,要证原式成立即证 ![]() 成立,
成立,
现证明:对任意x>0,g(x)<1+e﹣2恒成立,
当x≥1时,由(1)知g(x)≤0<1+e﹣2成立;
当0<x<1时,ex>1,且由(1)知g(x)>0,
∴ ![]() .
.
设F(x)=1﹣xlnx﹣x,x∈(0,1),则F'(x)=﹣(lnx+2),
当x∈(0,e﹣2)时,F′(x)>0,
当x∈(e﹣2,1)时,F′(x)<0,
所以当x=e﹣2时,F(x)取得最大值F(e﹣2)=1+e﹣2.
所以g(x)<F(x)≤1+e﹣2,即0<x<1时,g(x)<1+e﹣2.
综上所述,对任意x>0,g(x)<1+e﹣2.①
令G(x)=ex﹣x﹣1(x>0),则G'(x)=ex﹣1>0恒成立,
所以G(x)在(0,+∞)上递增,G(x)>G(0)=0恒成立,
即ex>x+1>0,即 ![]() .②
.②
当x≥1时,有: ![]() ;
;
当0<x<1时,由①②式, ![]() ,
,
综上所述,x>0时, ![]() 成立,
成立,
故原不等式成立
【解析】(1)求出f(x)的导数,通过解关于导函数的不等式,求出函数的单调区间即可;(2)问题转化为证 ![]() 成立,从而证明
成立,从而证明 ![]() ,设F(x)=1﹣xlnx﹣x,根据函数的单调性证明即可.
,设F(x)=1﹣xlnx﹣x,根据函数的单调性证明即可.
【考点精析】通过灵活运用利用导数研究函数的单调性,掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减即可以解答此题.
在这个区间单调递减即可以解答此题.

 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案