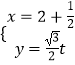题目内容
【题目】设α是空间中的一个平面,l,m,n是三条不同的直线,则下列命题中正确的是( )
A.若mα,nα,l⊥m,l⊥n,则l⊥α
B.若mα,n⊥α,l⊥n,则l∥m
C.若l∥m,m⊥α,n⊥α,则l∥n
D.若l⊥m,l⊥n,则n∥m
【答案】C
【解析】解:对于A,根据线面垂直的判定,当m,n相交时,结论成立,故A不正确;
对于B,mα,n⊥α,则n⊥m,∵l⊥n,∴可以选用正方体模型,可得l,m平行、相交、异面都有可能,如图所示,故B不正确;
对于C,由垂直于同一平面的两直线平行得m∥n,再根据平行线的传递性,即可得l∥n,故C正确;
对于D,l⊥m,l⊥n,则n、m平行、相交、异面均有可能,故D不正确
故选C.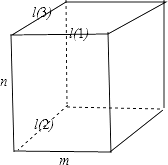
【考点精析】根据题目的已知条件,利用空间中直线与直线之间的位置关系和空间中直线与平面之间的位置关系的相关知识可以得到问题的答案,需要掌握相交直线:同一平面内,有且只有一个公共点;平行直线:同一平面内,没有公共点;异面直线: 不同在任何一个平面内,没有公共点;直线在平面内—有无数个公共点;直线与平面相交—有且只有一个公共点;直线在平面平行—没有公共点.

 名校课堂系列答案
名校课堂系列答案【题目】某奶茶店为了解白天平均气温与某种饮料销量之间的关系进行分析研究,记录了2月21日至2月25日
的白天平均气温x(℃)与该奶茶店的这种饮料销量y(杯),得到如表数据:
平均气温x(℃) | 9 | 11 | 12 | 10 | 8 |
销量y(杯) | 23 | 26 | 30 | 25 | 21 |
(1)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程 ![]() =
= ![]() x+
x+ ![]() ;
;
(2)试根据(1)求出的线性回归方程,预测平均气温约为20℃时该奶茶店的这种饮料销量.
(参考: ![]() =
=  ,
, ![]() =
= ![]() ﹣
﹣ ![]()
![]() ;9×23+11×26+12×30+10×25+8×21=1271,92+112+122+102+82=510)
;9×23+11×26+12×30+10×25+8×21=1271,92+112+122+102+82=510)