题目内容
18.已知袋子中有编号为1,2,3,4,5,6的6个红球,编号为1,2,3,4的4个白球,一次性从中摸出3个球.(1)求含有两种颜色的球的不同取法有多少种?
(2)求恰含有两种颜色且编号都不同的球的概率.
分析 (1),利用直接法,分类,1个红球2个白球或2个红球一个白球,或间接法,先求出没有限制的种数,再排除全是红球的和全是白球的,问题得以解决;
(2)分类,1个白球2个红球或2个白球一个红球,共有C41C52+C42C51=64,根据概率公式计算即可.
解答 解:(1)间接法:$C_{10}^3-C_6^3-C_4^3=120-20-4=96$,
直接法:$C_6^1•C_4^2+C_6^2•C_4^1=36+60=96$(种)
(2)没有限制的种数为C103=120,恰含有两种颜色且编号都不同的球,分类,1个白球2个红球或2个白球一个红球,共有C41C52+C42C51=64,
故恰含有两种颜色且编号都不同的球的概率为P=$\frac{64}{120}$=$\frac{8}{15}$.
点评 本题考查古典概型以及分类计数原理,属于中档题.

练习册系列答案
相关题目
8.设角θ的终边经过点P(4,-3),那么2cosθ-sinθ=( )
| A. | 1 | B. | $\frac{11}{5}$ | C. | $-\frac{11}{5}$ | D. | -1 |
6.若函数y=2exsinx,则y′=( )
| A. | -2excosx | B. | 2ex(sinx-cosx) | C. | -2exsinx | D. | 2ex(sinx+cosx) |
10.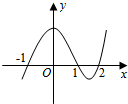 设函数f(x)在R上可导,其导函数为f′(x),且函数y=(2-x)f′(x)的图象如图所示,则下列结论中一定成立的是( )
设函数f(x)在R上可导,其导函数为f′(x),且函数y=(2-x)f′(x)的图象如图所示,则下列结论中一定成立的是( )
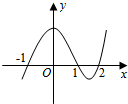 设函数f(x)在R上可导,其导函数为f′(x),且函数y=(2-x)f′(x)的图象如图所示,则下列结论中一定成立的是( )
设函数f(x)在R上可导,其导函数为f′(x),且函数y=(2-x)f′(x)的图象如图所示,则下列结论中一定成立的是( )| A. | 函数f(x)有极大值f(1)和极小值f(-1) | B. | 函数f(x)有极大值f(1)和极小值f(2) | ||
| C. | 函数f(x)有极大值f(2)和极小值f(1) | D. | 函数f(x)有极大值f(-1)和极小值f(2) |
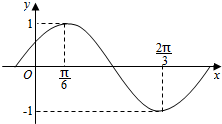 已知g(x)=f(x)-cos2x,函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)部分图象如图所示.
已知g(x)=f(x)-cos2x,函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)部分图象如图所示.