题目内容
15.某大型商厦一年内需要购进电脑5000台,每台电脑的价格为4000元,每次订购电脑的其它费用为1600元,年保管费用率为10%(例如,一年内平均库存量为150台,一年付出的保管费用60000元,则$\frac{60000}{150×4000}$=10%为年保管费用率),求每次订购多少台电脑,才能使订购电脑的其它费用及保管费用之和最小?分析 设每次订购电脑的台数为x,由题意可得每年的保管费用为$\frac{1}{2}$x•4000•10%元,每年的订货电脑的其它费用为$\frac{5000}{x}$•1600元,则有每年的总费用为y=$\frac{5000}{x}$•1600+$\frac{1}{2}$x•4000•10%元.运用导数求得极小值点,也为最小值点,可得最小值.
解答 解:设每次订购电脑的台数为x,
则开始库存量为x台,经过一个周期的正常均匀销售后,库存量变为零,
这样又开始下一次的订购,因此平均库存量为$\frac{1}{2}$x台,
所以每年的保管费用为$\frac{1}{2}$x•4000•10%元,
而每年的订货电脑的其它费用为$\frac{5000}{x}$•1600元,
这样每年的总费用为$\frac{5000}{x}$•1600+$\frac{1}{2}$x•4000•10%元.
令y=$\frac{5000}{x}$•1600+$\frac{1}{2}$x•4000•10%,
y′=-$\frac{1}{{x}^{2}}$•5000•1600+$\frac{1}{2}$•4000•10%.
令y′=0,解得x=200(台).
当x>200时,y′>0,当0<x<200时,y′<0,
也就是当x=200台时,每年订购电脑的其它费用及保管费用总费用达到最小值,
最小值为80000元.
点评 本题考查函数的最值的求法,主要运用导数判断单调性进而得到最值,由题意得到函数的解析式是解题的关键.

练习册系列答案
相关题目
6.若函数y=2exsinx,则y′=( )
| A. | -2excosx | B. | 2ex(sinx-cosx) | C. | -2exsinx | D. | 2ex(sinx+cosx) |
10.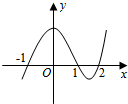 设函数f(x)在R上可导,其导函数为f′(x),且函数y=(2-x)f′(x)的图象如图所示,则下列结论中一定成立的是( )
设函数f(x)在R上可导,其导函数为f′(x),且函数y=(2-x)f′(x)的图象如图所示,则下列结论中一定成立的是( )
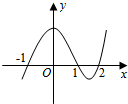 设函数f(x)在R上可导,其导函数为f′(x),且函数y=(2-x)f′(x)的图象如图所示,则下列结论中一定成立的是( )
设函数f(x)在R上可导,其导函数为f′(x),且函数y=(2-x)f′(x)的图象如图所示,则下列结论中一定成立的是( )| A. | 函数f(x)有极大值f(1)和极小值f(-1) | B. | 函数f(x)有极大值f(1)和极小值f(2) | ||
| C. | 函数f(x)有极大值f(2)和极小值f(1) | D. | 函数f(x)有极大值f(-1)和极小值f(2) |
20.曲线x2+y2=1经过伸缩变换$\left\{\begin{array}{l}{x′=\frac{1}{5}x}\\{y′=\frac{1}{3}y}\end{array}\right.$后,变成的曲线方程是( )
| A. | 25x2+9y2=1 | B. | 9x2+25y2=1 | C. | 25x+9y=1 | D. | $\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1 |
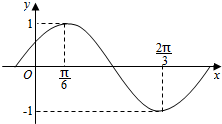 已知g(x)=f(x)-cos2x,函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)部分图象如图所示.
已知g(x)=f(x)-cos2x,函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)部分图象如图所示.