题目内容
17.原点与点(2,3)在直线2x+y-3=0的( )| A. | 同侧 | B. | (2,3)在直线上 | C. | 异侧 | D. | 以上都不对 |
分析 分别判断原点和(2,3)在式子2x+y-3的符号即可得到结论.
解答 解:当x=0,y=0时,2x+y-3=-3<0,
当x=2,y=3时,2x+y-3=4+3-3=4>0,
则原点与点(2,3)在直线2x+y-3=0的异侧,
故选:C
点评 本题主要考查点与直线位置关系的判断,比较基础.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
8.设角θ的终边经过点P(4,-3),那么2cosθ-sinθ=( )
| A. | 1 | B. | $\frac{11}{5}$ | C. | $-\frac{11}{5}$ | D. | -1 |
12.已知函数f(x)=$\frac{1}{3}$x3-(4m-1)x2+(15m2-2m-7)x+2在R上是增函数,则m的取值范围为( )
| A. | m≤2或m≥4 | B. | -4≤m≤-2 | C. | 2≤m≤4 | D. | 以上皆不对 |
6.若函数y=2exsinx,则y′=( )
| A. | -2excosx | B. | 2ex(sinx-cosx) | C. | -2exsinx | D. | 2ex(sinx+cosx) |
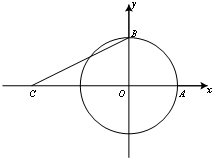 如图,曲线Γ:x2+y2=1分别与x、y轴的正半轴交于点A、B,点C(-2,0),角α、β的终边分别与曲线Γ交于点P、Q.
如图,曲线Γ:x2+y2=1分别与x、y轴的正半轴交于点A、B,点C(-2,0),角α、β的终边分别与曲线Γ交于点P、Q.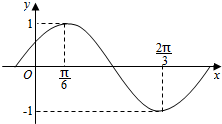 已知g(x)=f(x)-cos2x,函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)部分图象如图所示.
已知g(x)=f(x)-cos2x,函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)部分图象如图所示.