题目内容
12.求下列函数的导数:(1)f(x)=xtanx;
(2)f(x)=(x-1)(x-2)(x-3);
(3)f(x)=2sin3x.
分析 根据函数的导数公式分别进行求导即可.
解答 解:(1)函数的f(x)的导数f′(x)=x′tanx+x(tanx)′=tanx+$\frac{x}{co{s}^{2}x}$.
(2)函数的f(x)=x3-6x2+11x-6.
则f′(x)=3x2-12x+11.
(3)函数的f(x)的导数f′(x)=2cos3x•(3x)′=2×2cos3x=6cos3x.
点评 本题主要考查函数的导数的计算,要求熟练掌握掌握常见函数的导数公式,比较基础.

练习册系列答案
相关题目
20.曲线x2+y2=1经过伸缩变换$\left\{\begin{array}{l}{x′=\frac{1}{5}x}\\{y′=\frac{1}{3}y}\end{array}\right.$后,变成的曲线方程是( )
| A. | 25x2+9y2=1 | B. | 9x2+25y2=1 | C. | 25x+9y=1 | D. | $\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1 |
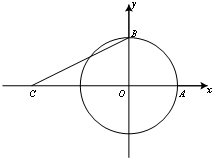 如图,曲线Γ:x2+y2=1分别与x、y轴的正半轴交于点A、B,点C(-2,0),角α、β的终边分别与曲线Γ交于点P、Q.
如图,曲线Γ:x2+y2=1分别与x、y轴的正半轴交于点A、B,点C(-2,0),角α、β的终边分别与曲线Γ交于点P、Q.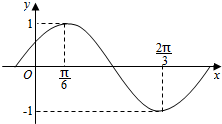 已知g(x)=f(x)-cos2x,函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)部分图象如图所示.
已知g(x)=f(x)-cos2x,函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)部分图象如图所示.