题目内容
19.设Sn是等差数列{an}的前n项和,已知$\frac{1}{3}$S3,$\frac{1}{4}$S4的等比中项为$\frac{1}{5}$S5;$\frac{1}{3}$S3,$\frac{1}{4}$S4的等差中项为1,求数列{an}的通项公式.分析 设等差数列{an}的首项a1=a,公差为d,则Sn=na+$\frac{n(n-1)}{2}$d,再由等比数列和等差数列的中项的性质,列方程,解方程可得a,d,再由等差数列的通项公式即可得到.
解答 解:设等差数列{an}的首项a1=a,公差为d,
则Sn=na+$\frac{n(n-1)}{2}$d,依题意,有
$\left\{\begin{array}{l}{\frac{1}{3}(3a+3d)•\frac{1}{4}(4a+6d)=\frac{1}{25}(5a+10d)^{2}}\\{\frac{1}{3}(3a+3d)+\frac{1}{4}(4a+6d)=2}\end{array}\right.$,即为$\left\{\begin{array}{l}{3ad+5{d}^{2}=0}\\{2a+\frac{5}{2}d=2}\end{array}\right.$,
∴a=1,d=0或a=4,d=-$\frac{12}{5}$.
∴an=1或an=$\frac{32}{5}$-$\frac{12}{5}$n,
经检验,an=1和an=$\frac{32}{5}$-$\frac{12}{5}$n均合题意.
∴所求等差数列的通项公式为an=1或an=$\frac{32}{5}$-$\frac{12}{5}$n.
点评 本题考查等差数列和等比数列的性质,同时考查等差数列的通项和求和公式的运用,属于中档题.

练习册系列答案
相关题目
10.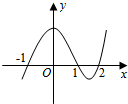 设函数f(x)在R上可导,其导函数为f′(x),且函数y=(2-x)f′(x)的图象如图所示,则下列结论中一定成立的是( )
设函数f(x)在R上可导,其导函数为f′(x),且函数y=(2-x)f′(x)的图象如图所示,则下列结论中一定成立的是( )
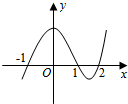 设函数f(x)在R上可导,其导函数为f′(x),且函数y=(2-x)f′(x)的图象如图所示,则下列结论中一定成立的是( )
设函数f(x)在R上可导,其导函数为f′(x),且函数y=(2-x)f′(x)的图象如图所示,则下列结论中一定成立的是( )| A. | 函数f(x)有极大值f(1)和极小值f(-1) | B. | 函数f(x)有极大值f(1)和极小值f(2) | ||
| C. | 函数f(x)有极大值f(2)和极小值f(1) | D. | 函数f(x)有极大值f(-1)和极小值f(2) |
9.已知向量$\vec a$=(1,n),$\vec b$=(-1,n),$\vec a$垂直于$\vec b$,则|${\vec a}$|=( )
| A. | 1 | B. | $\frac{\sqrt{6}}{2}$ | C. | $\sqrt{2}$ | D. | 4 |
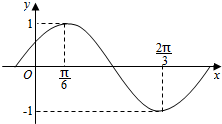 已知g(x)=f(x)-cos2x,函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)部分图象如图所示.
已知g(x)=f(x)-cos2x,函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)部分图象如图所示.